What Is 5 Of 30
sportsmenna
Sep 20, 2025 · 5 min read
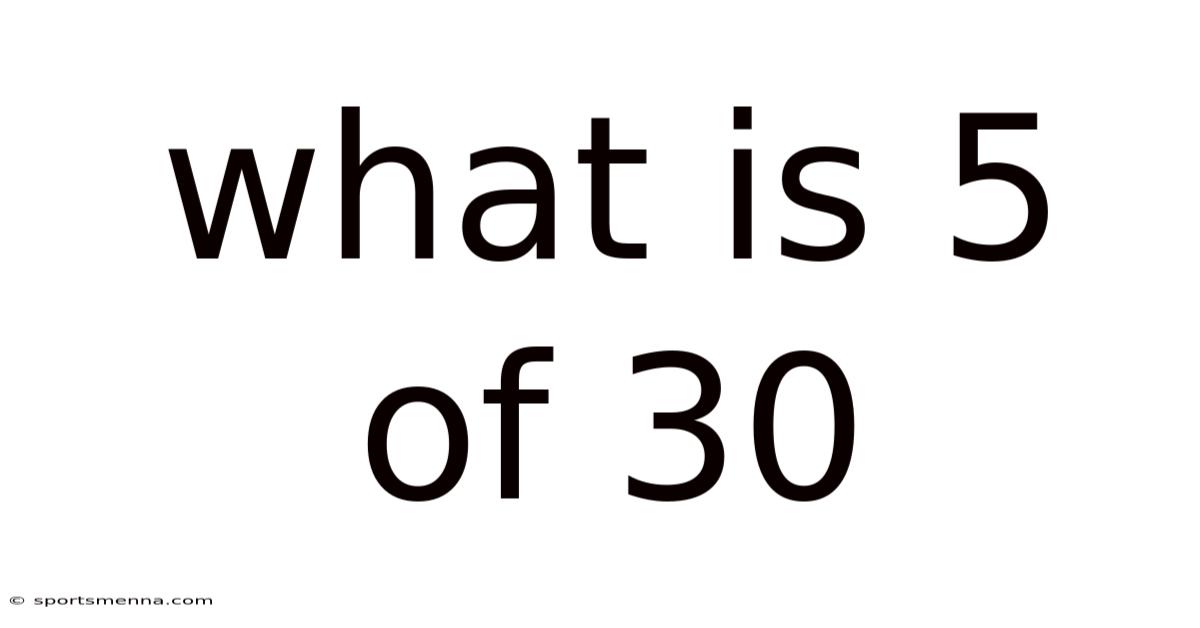
Table of Contents
What is 5 of 30? Understanding Fractions, Percentages, and Ratios
What does "5 of 30" mean? At first glance, it seems simple: five out of thirty. But this seemingly straightforward phrase opens a door to a world of mathematical concepts, including fractions, percentages, and ratios. Understanding these concepts is crucial for various aspects of life, from calculating discounts to understanding statistical data. This article will explore the meaning of "5 of 30" in detail, explaining the different ways to represent it and demonstrating its applications.
Understanding the Basics: Fractions, Percentages, and Ratios
Before diving into "5 of 30," let's clarify the fundamental concepts:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
-
Percentages: A percentage is a fraction expressed as a number out of 100. It represents a proportion of a whole and is denoted by the symbol %. For example, 50% means 50 out of 100, or 1/2.
-
Ratios: A ratio compares the quantities of two or more things. It can be expressed using a colon (e.g., 5:25) or as a fraction (e.g., 5/25). Ratios show the relative sizes of different quantities.
Representing "5 of 30"
"5 of 30" can be represented in several ways, each with its own advantages and applications:
-
Fraction: The most straightforward representation is a fraction: 5/30. This clearly shows that 5 is a part of a total of 30.
-
Simplified Fraction: The fraction 5/30 can be simplified by finding the greatest common divisor (GCD) of 5 and 30, which is 5. Dividing both the numerator and the denominator by 5, we get the equivalent fraction 1/6. This simplified fraction is easier to understand and use in calculations.
-
Decimal: To express "5 of 30" as a decimal, we divide the numerator (5) by the denominator (30): 5 ÷ 30 = 0.16666... (recurring decimal). This decimal representation is useful in calculations involving other decimals.
-
Percentage: To convert the fraction 5/30 (or 1/6) to a percentage, we divide the numerator by the denominator and multiply by 100: (5/30) * 100 = 16.67% (approximately). This representation is particularly helpful for showing proportions relative to a whole.
-
Ratio: "5 of 30" can also be expressed as a ratio: 5:30. This is equivalent to the fraction 5/30 and can be simplified to 1:6. Ratios are often used to compare quantities or proportions.
Applications of "5 of 30"
Understanding how to represent and interpret "5 of 30" is valuable in many real-world scenarios:
-
Calculating Test Scores: If a student answered 5 questions correctly out of a total of 30, their score would be 5/30 or 1/6, which is approximately 16.67%.
-
Analyzing Survey Results: If 5 out of 30 respondents chose a particular option in a survey, this represents 16.67% of the respondents.
-
Determining Proportions in Recipes: If a recipe calls for 30 units of an ingredient and you only want to make a smaller portion using 5 units, you are using 1/6 of the original recipe.
-
Understanding Probabilities: If there are 30 equally likely outcomes in an event, and 5 of those outcomes are favorable, the probability of a favorable outcome is 5/30 or 1/6.
-
Financial Calculations: Imagine you invested $30 and earned a profit of $5. Your return on investment is 5/30 or 1/6, approximately 16.67%.
Further Exploration: Working with Fractions
Working with fractions is a fundamental skill. Let's delve deeper into operations involving fractions, using the example of 5/30 (or 1/6):
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. For example, adding 1/6 + 1/3 requires changing 1/3 to 2/6, so the sum becomes 1/6 + 2/6 = 3/6 = 1/2.
-
Multiplying Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together. For example, (1/6) * (2/3) = 2/18 = 1/9.
-
Dividing Fractions: Dividing fractions involves inverting the second fraction and then multiplying. For example, (1/6) ÷ (2/3) = (1/6) * (3/2) = 3/12 = 1/4.
The Importance of Simplification
Simplifying fractions like 5/30 to 1/6 is crucial for several reasons:
-
Clarity: Simplified fractions are easier to understand and interpret. 1/6 is more intuitive than 5/30.
-
Efficiency: Simplified fractions make calculations simpler and less prone to errors.
-
Comparison: Comparing simplified fractions is much easier than comparing unsimplified ones. For example, comparing 1/6 to 1/3 is simpler than comparing 5/30 to 10/30.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a ratio and a fraction?
A1: While both ratios and fractions express relationships between numbers, fractions represent parts of a whole, while ratios compare the quantities of two or more things. They are closely related; a ratio can be expressed as a fraction.
Q2: How do I convert a fraction to a percentage?
A2: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, 1/6 = (1 ÷ 6) * 100 ≈ 16.67%.
Q3: Why is simplifying fractions important?
A3: Simplifying fractions makes them easier to understand, work with, and compare. It also reduces the risk of calculation errors.
Q4: Can I use a calculator to solve fraction problems?
A4: Yes, most calculators can handle fraction calculations. Some calculators even allow you to input and simplify fractions directly.
Q5: What are some real-world applications of understanding fractions and percentages?
A5: Numerous real-world applications exist, including calculating discounts, understanding financial statements, analyzing statistical data, measuring ingredients in cooking, and determining probabilities.
Conclusion
"5 of 30," seemingly a simple phrase, offers a rich opportunity to explore fundamental mathematical concepts. Understanding how to represent this phrase as a fraction, decimal, percentage, and ratio is crucial for navigating various aspects of daily life and solving a wide range of problems. Mastering these concepts empowers you to interpret data, make informed decisions, and confidently tackle numerical challenges. By practicing these techniques and exploring further mathematical concepts, you'll enhance your problem-solving skills and gain a deeper understanding of the world around you. Remember, the key is to practice regularly and apply these concepts to real-world situations to build a solid foundation in mathematics.
Latest Posts
Latest Posts
-
Spanish Words Beginning With W
Sep 20, 2025
-
167cm In Ft And Inches
Sep 20, 2025
-
What Is 25 Of 80
Sep 20, 2025
-
How Many Inches Is 150mm
Sep 20, 2025
-
Fish Names Starting With K
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.