What Is 25 Of 80
sportsmenna
Sep 20, 2025 · 5 min read
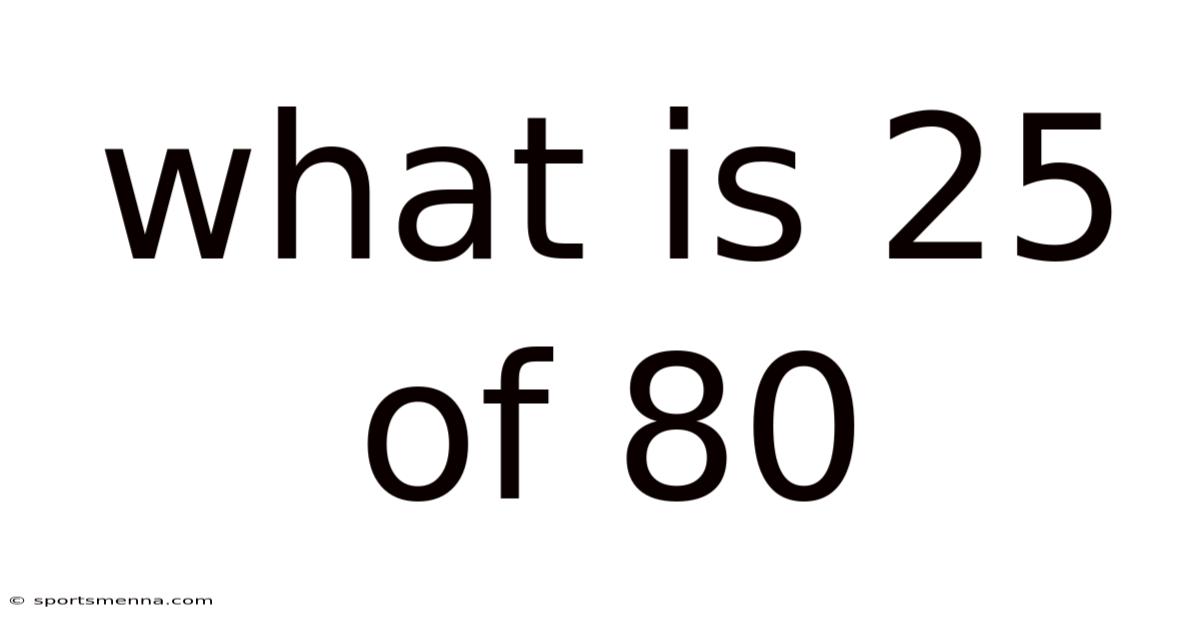
Table of Contents
What is 25% of 80? A Deep Dive into Percentages and Their Applications
Finding 25% of 80 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to calculate percentages and the underlying concepts has far-reaching applications in various fields, from everyday budgeting to complex financial modeling. This article will not only answer the question "What is 25% of 80?" but also delve into the broader world of percentage calculations, providing you with the tools to tackle similar problems with confidence. We will explore different methods for solving this problem, explain the underlying mathematical principles, and illustrate its practical significance.
Understanding Percentages: The Foundation
A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 25% can be written as 25/100 or 0.25 as a decimal. This simple representation is the key to understanding how to calculate percentages.
The fundamental formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
Method 1: Direct Calculation
Let's apply this formula directly to find 25% of 80:
(25/100) * 80 = 20
Therefore, 25% of 80 is 20.
Method 2: Using Decimal Equivalents
As mentioned earlier, 25% is equivalent to 0.25. We can use this decimal equivalent to simplify the calculation:
0.25 * 80 = 20
This method is often quicker and easier, particularly when dealing with percentages that have simple decimal equivalents, such as 10%, 25%, 50%, and 75%.
Method 3: Fractional Equivalents
Percentages can also be represented as fractions. 25% is equivalent to ¼ (one-quarter). Using this fractional equivalent, the calculation becomes:
(1/4) * 80 = 20
This method highlights the relationship between fractions and percentages, offering another perspective on the calculation.
Method 4: Using Proportions
We can solve this problem using proportions. We can set up a proportion where x represents the unknown value (25% of 80):
25/100 = x/80
To solve for x, we can cross-multiply:
25 * 80 = 100 * x
2000 = 100x
x = 2000/100
x = 20
This method demonstrates a more formal approach to solving percentage problems, especially useful when dealing with more complex scenarios.
Expanding the Understanding: Applications of Percentages
The ability to calculate percentages is a crucial life skill with broad applications:
-
Finance: Calculating interest on loans, savings accounts, and investments. Determining discounts on purchases, understanding tax rates, and analyzing financial statements all rely heavily on percentage calculations. For example, if you get a 15% discount on a $100 item, you'll save $15.
-
Statistics: Percentages are fundamental to understanding and interpreting statistical data. For instance, representing survey results, analyzing population demographics, and understanding probabilities all involve working with percentages. Consider a survey where 60% of respondents prefer a particular product; this concisely conveys important information.
-
Science: Percentages are used extensively in scientific research to express concentrations, error margins, and changes in experimental data. For example, a scientist might report that a certain chemical solution is 5% acid.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices in stores, and even comparing the nutritional value of different foods often require percentage calculations.
-
Business: Profit margins, sales growth, market share, and return on investment are all expressed as percentages, making them key performance indicators for businesses. A company might aim for a 10% increase in sales year-over-year.
Beyond the Basics: Calculating Other Percentages
The methods outlined above can be applied to calculate any percentage of any number. For example, let's find 30% of 150:
(30/100) * 150 = 45
Or, using the decimal equivalent:
0.30 * 150 = 45
Dealing with More Complex Percentages
While the examples above involve straightforward percentages, more complex calculations might involve multiple percentage changes or combined percentages. For example, calculating compound interest requires understanding how percentages accumulate over time.
Let's consider a scenario where an initial investment of $100 earns 5% interest annually for three years.
- Year 1: $100 * 0.05 = $5 interest; Total = $105
- Year 2: $105 * 0.05 = $5.25 interest; Total = $110.25
- Year 3: $110.25 * 0.05 = $5.51 interest; Total = $115.76
Note how the interest earned each year is based on the accumulated amount from the previous year, reflecting the compounding effect.
Frequently Asked Questions (FAQ)
-
Q: What if I need to find a percentage of a number that isn't a whole number?
-
A: The same methods apply. For example, to find 25% of 80.5, you would calculate (25/100) * 80.5 = 20.125.
-
Q: How do I calculate the percentage increase or decrease between two numbers?
-
A: To calculate the percentage increase, subtract the original number from the new number, divide the result by the original number, and multiply by 100. For percentage decrease, the process is the same but the result will be negative. For example, if a value increases from 50 to 60, the percentage increase is [(60-50)/50] * 100 = 20%.
-
Q: Are there any online calculators or tools to help with percentage calculations?
-
A: Yes, many online calculators are available to perform percentage calculations quickly and accurately.
Conclusion: Mastering Percentages for Success
Finding 25% of 80 is a simple calculation, resulting in 20. However, the significance extends far beyond this single problem. A solid understanding of percentages is an invaluable skill applicable across numerous disciplines and everyday scenarios. Mastering these concepts empowers you to navigate financial decisions, interpret data, and solve problems effectively. By understanding the underlying principles and various calculation methods, you can confidently tackle a wide range of percentage problems, paving the way for success in both personal and professional life. Remember the core formula and choose the method that best suits your needs and the complexity of the problem at hand. Practice regularly, and you will soon find yourself adept at handling any percentage calculation thrown your way.
Latest Posts
Latest Posts
-
Convert 5 4 To A Decimal
Sep 20, 2025
-
What Do I Feed Ladybugs
Sep 20, 2025
-
What Day Was You Born
Sep 20, 2025
-
What Dialling Code Is 0203
Sep 20, 2025
-
Meaning Of Ayaan In Islam
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.