What Is 25 Of 10
sportsmenna
Sep 22, 2025 · 6 min read
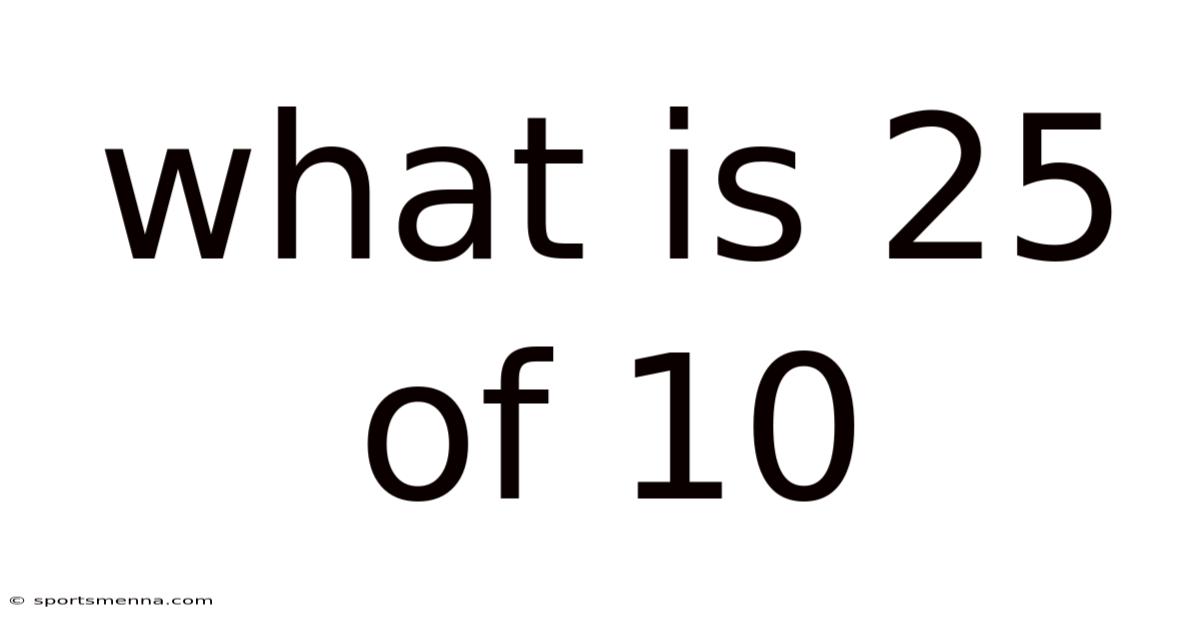
Table of Contents
Decoding "25 of 10": Understanding Fractions, Percentages, and Ratios
What does "25 of 10" actually mean? At first glance, it might seem nonsensical. We're used to hearing phrases like "25 out of 100" or "25 percent," but "25 of 10" requires a deeper understanding of mathematical concepts like fractions, percentages, and ratios. This article will delve into the meaning of this phrase, explore the underlying mathematical principles, and provide practical examples to solidify your understanding. We will uncover how this seemingly unusual expression can be interpreted and used in various contexts.
Understanding the Core Concepts: Fractions, Percentages, and Ratios
Before we tackle "25 of 10," let's refresh our understanding of the three core mathematical concepts that will help us decipher its meaning:
1. Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, while the numerator indicates how many of those parts are being considered. For example, 1/2 (one-half) means one part out of two equal parts.
2. Percentages: A percentage is a way of expressing a fraction or ratio as a portion of 100. It's denoted by the symbol "%". For instance, 50% means 50 parts out of 100, which is equivalent to the fraction 50/100 or 1/2. Percentages are commonly used to represent proportions, changes, and rates.
3. Ratios: A ratio is a comparison of two or more quantities. It can be expressed in different forms: using the colon symbol (e.g., 2:3), as a fraction (e.g., 2/3), or using the word "to" (e.g., 2 to 3). Ratios are useful in comparing sizes, proportions, and rates.
Interpreting "25 of 10": The Ambiguity and Possible Meanings
The phrase "25 of 10" is inherently ambiguous. It doesn't directly follow standard mathematical notation. However, we can interpret it in a few ways, depending on the intended meaning:
1. Improper Fraction: One interpretation is to consider it as an improper fraction: 25/10. This fraction represents 25 parts out of a total of 10 parts. This is an improper fraction because the numerator is larger than the denominator. We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 5:
25/10 = (25 ÷ 5) / (10 ÷ 5) = 5/2
This simplified fraction, 5/2, is equivalent to 2.5 or two and a half.
2. Ratio: Another interpretation is to consider "25 of 10" as a ratio of 25 to 10, written as 25:10 or 25/10. Similar to the improper fraction interpretation, this ratio simplifies to 5:2 or 5/2, representing a ratio of 5 to 2. This could represent a comparison between two quantities, such as the ratio of red balls to blue balls in a bag. For every 2 blue balls, there are 5 red balls.
3. Percentage (with a Twist): While not a direct representation of a percentage, we can still manipulate the numbers to find a percentage. If we consider "25 of 10" as a fraction (25/10), we can convert it to a percentage by multiplying by 100%:
(25/10) * 100% = 250%
This means "25 of 10" can be interpreted as 250% of 10. This suggests that "25 of 10" represents a quantity that is 2.5 times larger than 10 (as 250% is equivalent to 2.5).
4. Context is Key: The true meaning of "25 of 10" heavily relies on the context in which it's used. Without further information or clarification, the phrase remains ambiguous.
Real-World Examples and Applications
Let's explore some real-world scenarios where interpretations of "25 of 10" might be relevant:
-
Scenario 1: Baking: Imagine a recipe calls for 10 cups of flour, but you accidentally add 25 cups. The ratio of flour added to the required amount is 25:10, simplifying to 5:2. You added 2.5 times the required amount of flour.
-
Scenario 2: Sales: A company’s sales target is 10 units, but they achieved 25 units. Their sales exceeded the target by 250%, achieving 2.5 times their goal.
-
Scenario 3: Sports: A basketball player attempts 10 shots and scores 25 points. This is not physically possible within standard basketball rules; therefore, it is likely a ratio representing points per attempt (2.5 points per attempt).
-
Scenario 4: Stock Market: A stock's value increases from 10 to 25. The increase represents a 150% growth ( (25-10)/10 * 100%). This example shows how interpreting the relationship between 10 and 25 can be contextualized.
Mathematical Explanations and Calculations
Let's solidify the mathematical aspects behind our different interpretations:
-
Converting Fractions to Decimals: To convert an improper fraction like 25/10 to a decimal, we perform the division: 25 ÷ 10 = 2.5
-
Converting Fractions to Percentages: To convert a fraction to a percentage, we multiply the fraction by 100%: (25/10) * 100% = 250%
-
Simplifying Ratios: To simplify a ratio like 25:10, we find the greatest common divisor (GCD) of 25 and 10, which is 5. We then divide both numbers by the GCD: 25 ÷ 5 = 5 and 10 ÷ 5 = 2. The simplified ratio is 5:2.
-
Working with Percentages: To find what 250% of 10 is, we multiply 10 by 2.5 (since 250% = 2.5): 10 * 2.5 = 25. This confirms our interpretation of 250% in the context of “25 of 10”.
Frequently Asked Questions (FAQs)
Q1: Is "25 of 10" a standard mathematical expression?
A1: No, it's not a standard mathematical expression. Standard mathematical notation would use fractions, ratios, or percentages to represent such relationships clearly. The ambiguity highlights the importance of precise language in mathematics.
Q2: Why is context important in understanding "25 of 10"?
A2: Context is crucial because the phrase itself lacks inherent meaning. The surrounding information determines whether it's an improper fraction, a ratio, or a representation of a percentage increase.
Q3: How can I avoid ambiguity when expressing such relationships?
A3: Always use clear and precise mathematical notation. Instead of "25 of 10," use either:
- 25/10 (fraction)
- 25:10 (ratio)
- 250% (percentage)
- 2.5 times more than 10
Q4: What if the context doesn't clarify the meaning?
A4: If the context doesn't provide clarity, seek clarification from the person who used the phrase. Avoid making assumptions about the intended meaning.
Conclusion: The Power of Precision in Mathematics
The seemingly simple phrase "25 of 10" reveals the importance of precision and clarity in mathematical communication. While we can explore different interpretations based on the underlying concepts of fractions, percentages, and ratios, the inherent ambiguity highlights the need for using standardized mathematical notation to avoid confusion. By understanding the core mathematical principles and applying them to real-world scenarios, we can effectively interpret and utilize numerical relationships, even when faced with unconventional phrasing. Remember that context is king, and clear communication is paramount in mathematics and all aspects of life. By avoiding ambiguous phrasing and employing clear mathematical language, we foster better understanding and reduce the risk of misinterpretations.
Latest Posts
Latest Posts
-
What Is A Bay Horse
Sep 22, 2025
-
Vegetables That Start With S
Sep 22, 2025
-
20 Percent As A Decimal
Sep 22, 2025
-
How Big Is One Meter
Sep 22, 2025
-
Aerobic Respiration Equation In Animals
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.