20 Percent As A Decimal
sportsmenna
Sep 22, 2025 · 6 min read
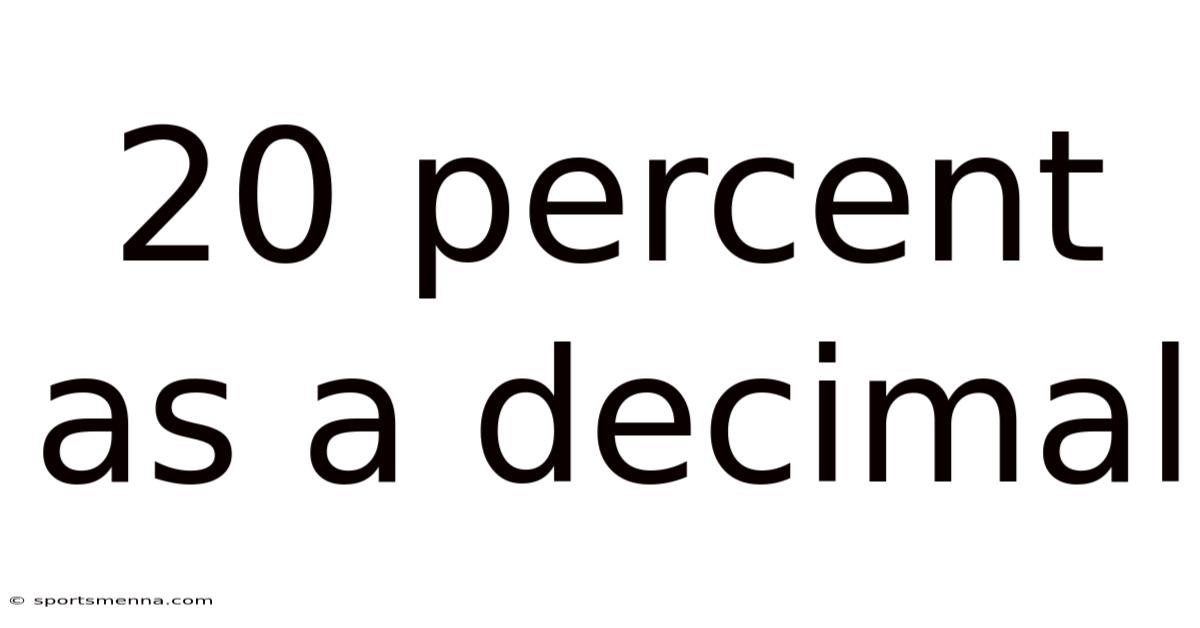
Table of Contents
20 Percent as a Decimal: A Comprehensive Guide
Understanding percentages is crucial in various aspects of life, from calculating discounts in a store to comprehending financial reports. This comprehensive guide will explore the conversion of percentages to decimals, specifically focusing on how to represent 20 percent as a decimal, and will delve into the broader concept of percentage-to-decimal conversion. We'll cover the underlying mathematical principles, explore practical applications, and address frequently asked questions, making this a valuable resource for students, professionals, and anyone seeking to improve their numerical literacy.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). So, 20 percent means 20 out of 100, or 20/100. This fractional representation is key to understanding the conversion to decimals.
Converting Percentages to Decimals: The Core Concept
The process of converting a percentage to a decimal is straightforward. You simply divide the percentage value by 100. This is because a percentage is fundamentally a fraction with a denominator of 100. Dividing by 100 is equivalent to moving the decimal point two places to the left.
Let's illustrate this with a simple example: To convert 50% to a decimal, we divide 50 by 100: 50 ÷ 100 = 0.5. Therefore, 50% is equal to 0.5 as a decimal.
20 Percent as a Decimal: A Step-by-Step Guide
Now, let's focus on the specific question: What is 20 percent as a decimal?
Following the same principle:
-
Start with the percentage: We have 20%.
-
Divide by 100: 20 ÷ 100 = 0.2
-
Result: 20% as a decimal is 0.2.
This simple calculation demonstrates the ease of converting percentages to decimals. The key is remembering the fundamental relationship between percentages and fractions with a denominator of 100.
Practical Applications of Percentage-to-Decimal Conversion
The ability to convert percentages to decimals is essential in numerous real-world scenarios:
-
Financial Calculations: Interest rates, discounts, tax calculations, and profit margins are often expressed as percentages. Converting them to decimals is crucial for accurate computations. For instance, calculating a 20% discount on a $100 item requires converting 20% to 0.2 and then multiplying: $100 * 0.2 = $20 discount.
-
Statistical Analysis: In statistics, percentages are frequently used to represent proportions and probabilities. Converting them to decimals simplifies statistical calculations and interpretations. For example, if a study shows a 20% success rate, this translates to a decimal probability of 0.2.
-
Scientific Calculations: Percentages are employed in various scientific fields, such as chemistry and physics, to express concentrations, efficiencies, and other quantitative measures. Converting to decimals ensures consistency in calculations and facilitates comparisons across different experimental settings.
-
Data Representation: Data visualization tools often require numerical data to be in decimal format. Converting percentages to decimals ensures compatibility with these tools, enabling effective data representation and analysis.
-
Everyday Life: Understanding percentage-to-decimal conversion can help you make informed decisions in everyday situations, such as comparing prices, understanding sales, or interpreting survey results.
Beyond 20 Percent: Converting Other Percentages to Decimals
The method described above applies to any percentage. Here are a few more examples:
- 5% as a decimal: 5 ÷ 100 = 0.05
- 75% as a decimal: 75 ÷ 100 = 0.75
- 125% as a decimal: 125 ÷ 100 = 1.25 (Note that percentages can be greater than 100%)
- 0.5% as a decimal: 0.5 ÷ 100 = 0.005 (Note that percentages can be less than 1%)
These examples further illustrate the consistent application of the division-by-100 method. This method simplifies the conversion process, making it accessible even without a calculator for simple percentages.
Converting Decimals to Percentages: The Reverse Process
It's equally important to understand the reverse process: converting decimals to percentages. This involves multiplying the decimal by 100 and adding a "%" symbol. For example, converting 0.25 to a percentage: 0.25 * 100 = 25%. This reciprocal process is crucial for verifying calculations and ensuring accuracy.
Advanced Applications and Considerations
While the basic conversion is straightforward, there are some more nuanced aspects to consider:
-
Rounding: When dealing with complex calculations involving percentages, rounding might be necessary to achieve a desired level of precision. Rounding rules should be applied consistently to maintain accuracy throughout the calculation process.
-
Significant Figures: In scientific and engineering contexts, paying close attention to significant figures is crucial to avoid propagating errors. The number of significant figures in the final result should reflect the precision of the input values.
-
Using Calculators and Software: Calculators and spreadsheet software (like Microsoft Excel or Google Sheets) offer built-in functions for percentage calculations, automating the conversion process and minimizing errors. Familiarity with these tools is highly beneficial for efficient and accurate calculations.
-
Working with Fractions: Remember, percentages are fundamentally fractions. Converting a fraction to a decimal, and then to a percentage is another useful skill to master. For instance, 1/4 is equivalent to 0.25, which is equal to 25%.
Frequently Asked Questions (FAQ)
Q: Can percentages be greater than 100%?
A: Yes, percentages can be greater than 100%. This indicates that a value is more than the reference value (the 100% value). For example, 150% means 1.5 times the reference value.
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, divide this difference by the original value, and multiply by 100. A percentage decrease is calculated similarly, but the difference will be negative.
Q: Why is understanding percentage-to-decimal conversion important?
A: It's crucial for accurate calculations in various fields, from finance and statistics to science and everyday life. It simplifies calculations and ensures consistent numerical representations.
Q: Are there any shortcuts for converting simple percentages to decimals?
A: Yes, for simple percentages, you can often perform the division mentally by moving the decimal point two places to the left. For instance, 10% becomes 0.1, 5% becomes 0.05, and so on.
Q: What if I have a percentage with a decimal, such as 20.5%?
A: The process remains the same: divide by 100. 20.5 ÷ 100 = 0.205.
Conclusion
Converting 20 percent to its decimal equivalent, 0.2, is a fundamental skill with wide-ranging applications. This guide has detailed not only the simple calculation but also the underlying principles, practical applications, and common queries surrounding percentage-to-decimal conversions. Mastering this concept empowers individuals to perform various calculations efficiently and accurately in numerous contexts, furthering both numerical literacy and problem-solving skills. By understanding the relationship between percentages and decimals, one can confidently approach a wide variety of quantitative tasks in both academic and professional settings. Remember that practice is key to solidifying this essential mathematical skill.
Latest Posts
Latest Posts
-
How Do You Pronounce Omeprazole
Sep 22, 2025
-
What Speed Should Airbags Deploy
Sep 22, 2025
-
Kilometers Per Hour To Knots
Sep 22, 2025
-
What Language Does Chile Speak
Sep 22, 2025
-
4 Letter Words With Az
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.