Prime Factor Tree For 220
sportsmenna
Sep 21, 2025 · 5 min read
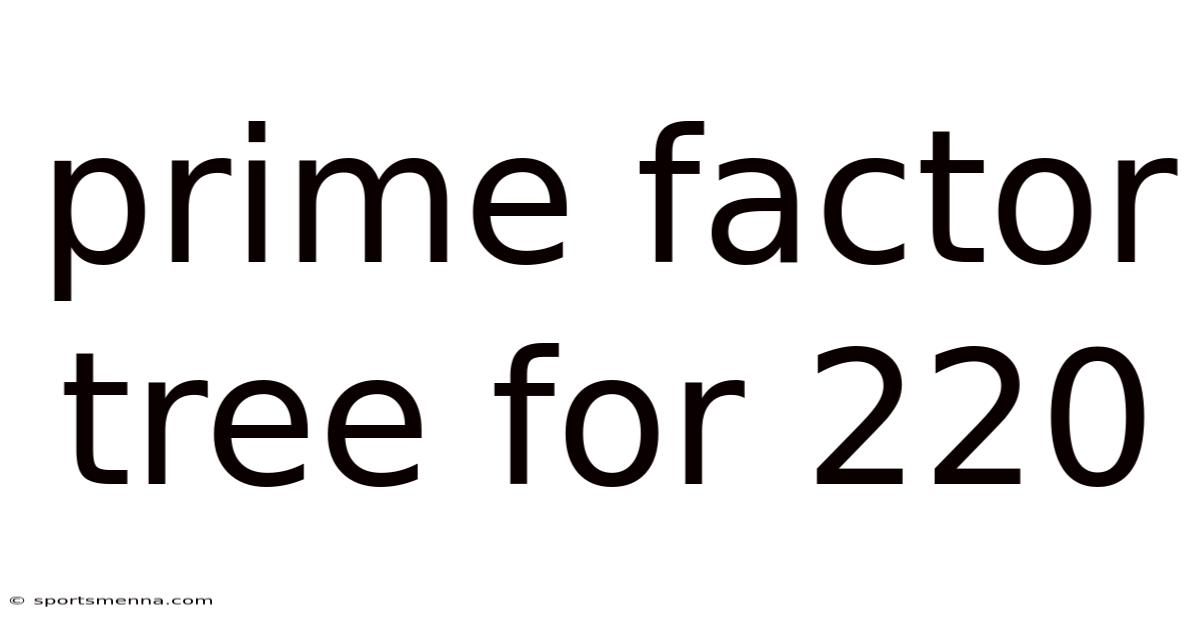
Table of Contents
Unveiling the Prime Factors of 220: A Deep Dive into Prime Factorization using Factor Trees
Finding the prime factors of a number might seem like a dry mathematical exercise, but it's a fundamental concept with far-reaching applications in number theory, cryptography, and even computer science. This article will guide you through the process of prime factorization, specifically focusing on the number 220, using the visual and intuitive method of the prime factor tree. We'll explore the steps involved, the underlying mathematical principles, and answer frequently asked questions to ensure a complete understanding. By the end, you'll not only know the prime factors of 220 but also grasp the broader concept of prime factorization and its significance.
Understanding Prime Numbers and Prime Factorization
Before we embark on our journey to find the prime factors of 220, let's solidify our understanding of some key terms. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. A number that is not prime is called a composite number.
Prime factorization, also known as prime decomposition, is the process of expressing a composite number as a product of its prime factors. Every composite number can be uniquely expressed as a product of prime numbers, a fact known as the Fundamental Theorem of Arithmetic. This uniqueness is crucial in various mathematical applications.
Constructing the Prime Factor Tree for 220
The prime factor tree is a visual tool that helps us systematically break down a composite number into its prime factors. Let's build the tree for 220:
-
Start with the number: Begin by writing the number 220 at the top of your tree.
-
Find a pair of factors: Identify any two numbers that multiply to give 220. For example, we can use 10 and 22. Write these numbers below 220, connecting them with branches.
-
Continue factoring: Now, we look at each of the factors (10 and 22) and see if they are prime or composite. 10 is composite (2 x 5), so we branch it further into 2 and 5. Similarly, 22 is composite (2 x 11), so we branch it into 2 and 11.
-
Terminate at prime numbers: Continue this process until all the branches end in prime numbers. In our case, we end up with 2, 5, 2, and 11.
Here's a visual representation of the prime factor tree for 220:
220
/ \
10 22
/ \ / \
2 5 2 11
Therefore, the prime factorization of 220 is 2 x 2 x 5 x 11, which can also be written as 2² x 5 x 11.
Alternative Factor Trees and the Uniqueness of Prime Factorization
It's important to note that you can create different prime factor trees for the same number, depending on the initial pair of factors you choose. For example, you could have started with 11 and 20, then broken down 20 further. However, regardless of the path you take in constructing the tree, you will always end up with the same set of prime factors. This highlights the Fundamental Theorem of Arithmetic – the prime factorization of a composite number is unique.
Mathematical Significance and Applications of Prime Factorization
The seemingly simple process of prime factorization has profound implications across various mathematical fields and practical applications:
-
Number Theory: Prime factorization is a cornerstone of number theory. Concepts like greatest common divisor (GCD) and least common multiple (LCM) rely heavily on the prime factorization of numbers. Understanding prime factorization helps us to solve problems involving divisibility and modular arithmetic.
-
Cryptography: Prime numbers play a crucial role in modern cryptography, especially in public-key cryptography systems like RSA. The security of these systems depends on the difficulty of factoring very large numbers into their prime factors. The larger the prime numbers, the more secure the system.
-
Computer Science: Algorithms for factoring large numbers are actively researched in computer science. Efficient factorization algorithms are essential for breaking certain cryptographic systems, but they are also used in other computational tasks.
-
Simplifying Fractions: Prime factorization is extremely useful for simplifying fractions to their lowest terms. By finding the prime factors of the numerator and denominator, we can cancel out common factors.
Beyond 220: Practice and Further Exploration
Understanding the prime factorization of 220 provides a strong foundation for tackling other numbers. Try constructing prime factor trees for different numbers, such as 36, 100, or 504. The more you practice, the more intuitive the process will become. Experiment with different starting factors to see how the tree structure changes while the final prime factors remain the same.
Frequently Asked Questions (FAQ)
Q1: What if a number is already prime?
A1: If the number is prime, the prime factor tree is trivial; the number itself is its only prime factor. For example, the prime factor tree for 7 would simply be 7.
Q2: Can I use a calculator to find prime factors?
A2: While calculators can help with division, building a prime factor tree is a valuable exercise that strengthens your understanding of prime numbers and factorization. However, some calculators and software have built-in prime factorization functions that can assist with larger numbers.
Q3: Are there any shortcuts for finding prime factors?
A3: Knowing divisibility rules for small prime numbers (2, 3, 5, 7, 11, etc.) can help speed up the process. For instance, if a number is even, it's divisible by 2. If the sum of its digits is divisible by 3, it's divisible by 3. These rules can help you identify initial factors more quickly.
Q4: Why is prime factorization important?
A4: Prime factorization is a fundamental concept in mathematics with applications in various fields, including cryptography, number theory, and computer science. It provides a unique representation of composite numbers and is essential for understanding divisibility, greatest common divisors, and least common multiples.
Conclusion
Finding the prime factors of 220, using the prime factor tree method, provides a clear illustration of prime factorization. This process is more than just a mathematical procedure; it's a foundational concept with significant implications in diverse fields. By understanding prime factorization, you gain a deeper appreciation of the structure of numbers and their interrelationships. Continue to practice and explore the world of prime numbers – you'll discover their fascinating properties and their importance in the world of mathematics and beyond. Remember, the seemingly simple act of breaking down a number into its prime constituents unlocks a wealth of mathematical knowledge and applications.
Latest Posts
Latest Posts
-
99 Degrees F To C
Sep 21, 2025
-
Average Speed Of A Snail
Sep 21, 2025
-
Cold Hands Warm Heart Meaning
Sep 21, 2025
-
Single Ready To Mingle Meaning
Sep 21, 2025
-
What Is 15 Of 200
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.