What Is 15 Of 200
sportsmenna
Sep 21, 2025 · 5 min read
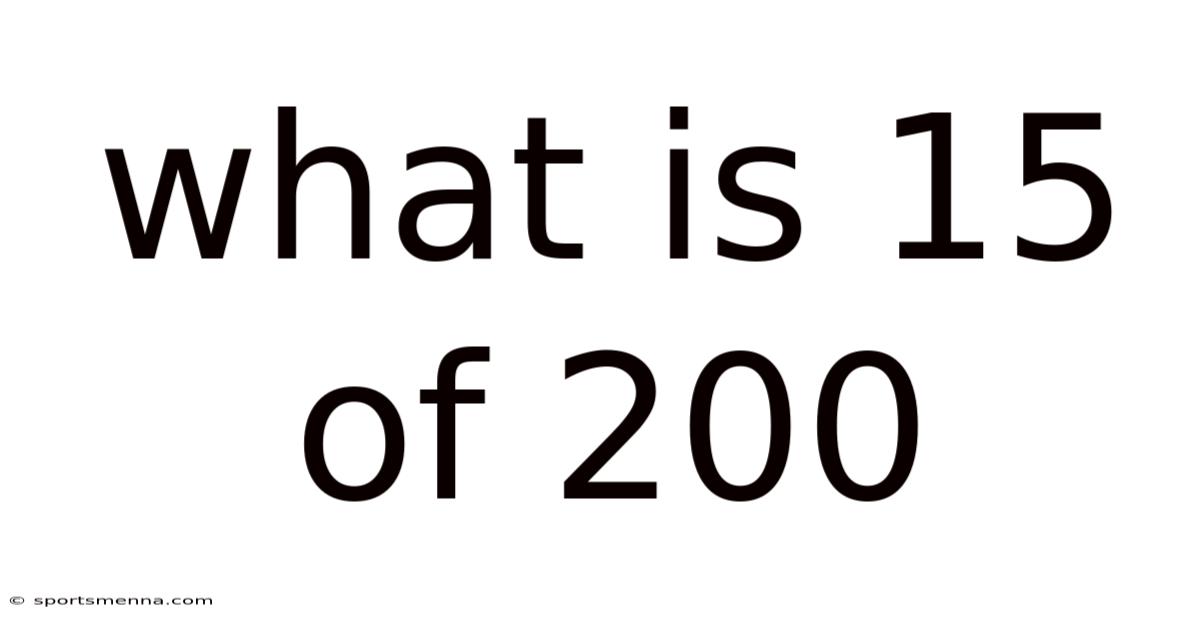
Table of Contents
What is 15% of 200? A Comprehensive Guide to Percentages and Their Applications
Finding 15% of 200 might seem like a simple arithmetic problem, but understanding the underlying principles of percentages is crucial for various applications in everyday life, from calculating discounts and tips to understanding financial statements and statistical data. This comprehensive guide will not only answer the question "What is 15% of 200?" but also delve into the broader concept of percentages, providing you with the tools and knowledge to tackle similar problems confidently.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ("per cent" from Latin). Therefore, 15% can be written as 15/100 or 0.15. Understanding this fundamental concept is key to solving percentage problems. Percentages are used extensively in various fields, including finance, statistics, science, and everyday life. They provide a standardized way to represent proportions and make comparisons easier. For instance, understanding percentage changes in stock prices, inflation rates, or population growth requires a solid grasp of percentage calculations.
Method 1: Calculating 15% of 200 using the Fraction Method
The most straightforward way to calculate 15% of 200 is to convert the percentage to a fraction and then multiply. Remember, 15% is equivalent to 15/100.
Therefore, the calculation is as follows:
(15/100) * 200 = 30
Therefore, 15% of 200 is 30.
Method 2: Calculating 15% of 200 using the Decimal Method
Alternatively, you can convert the percentage to a decimal and then multiply. As mentioned earlier, 15% is equal to 0.15.
The calculation becomes:
0.15 * 200 = 30
Again, we arrive at the answer: 15% of 200 is 30.
Method 3: Calculating 15% of 200 using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion:
15/100 = x/200
Where 'x' represents the unknown value (15% of 200). To solve for x, we can cross-multiply:
100x = 15 * 200
100x = 3000
x = 3000/100
x = 30
Using proportions, we confirm that 15% of 200 is 30.
Understanding the Different Methods: A Comparative Analysis
All three methods – the fraction method, the decimal method, and the proportion method – yield the same correct result. The choice of method often depends on personal preference and the specific context of the problem. The fraction method is conceptually clear and easy to understand, particularly for beginners. The decimal method is often faster for those comfortable with decimal calculations. The proportion method is useful when dealing with more complex percentage problems or when setting up comparative ratios.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations:
-
Shopping: Calculating discounts, sales tax, and tips. For example, if a shirt costs $200 and is on sale for 15% off, you would save $30 (15% of $200).
-
Finance: Determining interest earned on savings accounts or interest paid on loans. Understanding percentage changes in investments is crucial for financial planning.
-
Taxes: Calculating income tax, sales tax, and property tax. These calculations often involve percentages.
-
Statistics: Analyzing data sets and representing proportions. Percentages are frequently used in charts, graphs, and reports to represent proportions within a larger group.
-
Science: Expressing concentrations of solutions, error margins in experiments, and many other applications.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 200 is a relatively straightforward problem, understanding percentages extends to more complex scenarios:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two values. For example, if a quantity increases from 100 to 120, the percentage increase is 20% [(120-100)/100 * 100%].
-
Finding the original value after a percentage change: If a value is increased by 15% to become 230, the original value can be calculated using algebra.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. This is a more advanced application of percentages.
-
Percentage points vs. percentage change: It's important to distinguish between these two concepts. A percentage point represents a direct difference between two percentages, while a percentage change reflects the relative difference. For instance, an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest way depends on your comfort level with different mathematical operations. Many find converting the percentage to a decimal and multiplying the simplest approach.
Q2: How can I calculate percentages without a calculator?
A2: For simple percentages like 10%, 25%, or 50%, you can use mental math techniques. For more complex percentages, you can use the fraction method or break down the percentage into smaller, easier-to-calculate parts.
Q3: Are there any online tools to help calculate percentages?
A3: Yes, many websites and apps offer percentage calculators. These tools can be helpful for more complex calculations or for double-checking your work.
Q4: What are some common mistakes to avoid when calculating percentages?
A4: Common mistakes include incorrectly converting percentages to decimals or fractions, using the incorrect formula, and confusing percentage points with percentage change. Always double-check your work and ensure you understand the context of the problem.
Conclusion: Mastering Percentages for Everyday Success
Calculating 15% of 200, as we've demonstrated, is a relatively simple task. However, the underlying principles of percentage calculations are far-reaching and essential for navigating various aspects of life. Mastering these principles equips you with the tools to handle financial calculations, analyze data, understand statistics, and make informed decisions in numerous situations. By understanding the different methods available and practicing regularly, you can build confidence and proficiency in working with percentages, ultimately enhancing your problem-solving skills and decision-making abilities. Remember to practice regularly, starting with simple problems and gradually moving to more complex scenarios. The more you practice, the more confident and accurate you'll become in your percentage calculations.
Latest Posts
Latest Posts
-
Why Did Mendeleev Leave Gaps
Sep 21, 2025
-
He Who Hesitates Is Lost
Sep 21, 2025
-
Lcm Of 6 And 10
Sep 21, 2025
-
Food That Begin With Q
Sep 21, 2025
-
50 To 1 Gas Mixture
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.