Lcm Of 42 And 30
sportsmenna
Sep 21, 2025 · 6 min read
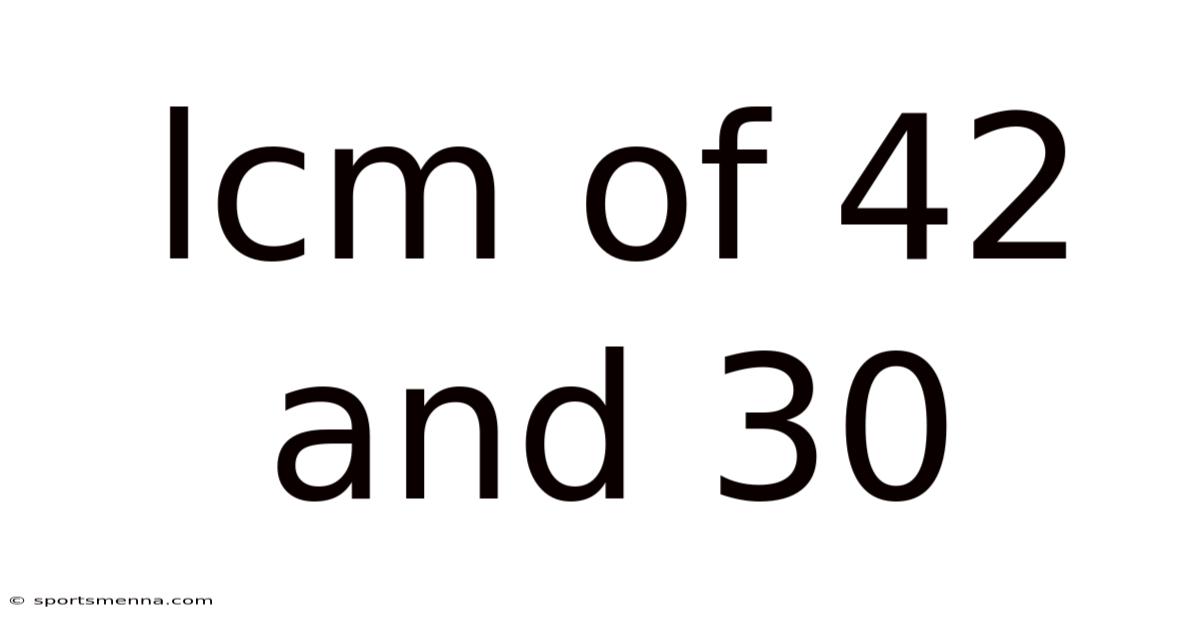
Table of Contents
Finding the Least Common Multiple (LCM) of 42 and 30: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and different methods for calculating it is crucial for a strong foundation in mathematics. This comprehensive guide will explore the LCM of 42 and 30, demonstrating various approaches and explaining the mathematical concepts involved. We'll move beyond simply finding the answer and delve into why these methods work, making this a valuable resource for students and anyone looking to refresh their understanding of number theory.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all of the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Understanding the LCM is essential in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like modular arithmetic.
In this article, we'll focus on finding the LCM of 42 and 30. We'll explore several methods, including using prime factorization, listing multiples, and employing the greatest common divisor (GCD).
Method 1: Prime Factorization
This is arguably the most efficient and insightful method for finding the LCM. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors).
Steps:
-
Find the prime factorization of each number:
- 42 = 2 x 3 x 7
- 30 = 2 x 3 x 5
-
Identify the highest power of each prime factor present in either factorization:
- The prime factors are 2, 3, 5, and 7.
- The highest power of 2 is 2¹
- The highest power of 3 is 3¹
- The highest power of 5 is 5¹
- The highest power of 7 is 7¹
-
Multiply the highest powers together:
LCM(42, 30) = 2¹ x 3¹ x 5¹ x 7¹ = 2 x 3 x 5 x 7 = 210
Therefore, the least common multiple of 42 and 30 is 210. This means 210 is the smallest positive integer that is divisible by both 42 and 30.
Method 2: Listing Multiples
This method is more intuitive but can be less efficient, especially when dealing with larger numbers. It involves listing the multiples of each number until a common multiple is found.
Steps:
-
List the multiples of 42: 42, 84, 126, 168, 210, 252, 294, 336, 378, 420...
-
List the multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300...
-
Identify the smallest common multiple: The smallest number that appears in both lists is 210.
Therefore, the LCM(42, 30) = 210. While this method works, it becomes cumbersome for larger numbers. It's best suited for smaller numbers where you can easily identify the common multiples.
Method 3: Using the Greatest Common Divisor (GCD)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD). The GCD of two integers is the largest integer that divides both numbers without leaving a remainder. There's a handy formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Steps:
-
Find the GCD of 42 and 30 using the Euclidean algorithm:
- Divide the larger number (42) by the smaller number (30): 42 = 30 x 1 + 12
- Replace the larger number with the remainder (12) and repeat: 30 = 12 x 2 + 6
- Repeat: 12 = 6 x 2 + 0
- The last non-zero remainder is the GCD: GCD(42, 30) = 6
-
Apply the LCM/GCD formula:
LCM(42, 30) = (42 x 30) / GCD(42, 30) = (42 x 30) / 6 = 210
Therefore, the LCM(42, 30) = 210. This method is efficient and provides a direct calculation using the GCD, which can be found relatively quickly using the Euclidean algorithm. The Euclidean algorithm is particularly powerful for finding the GCD of larger numbers.
A Deeper Dive: Understanding the Mathematics Behind the LCM
The LCM is deeply connected to the fundamental building blocks of numbers – prime numbers. The prime factorization method highlights this connection. Each number is broken down into its prime components, and the LCM is constructed by taking the highest power of each prime factor present in the factorization of either number. This ensures that the resulting number is divisible by both original numbers.
The relationship between the LCM and GCD is a fascinating aspect of number theory. The formula LCM(a, b) x GCD(a, b) = a x b elegantly links these two important concepts. It underscores the interconnectedness of divisibility properties within the number system.
Applications of LCM
The LCM has numerous applications across various fields:
-
Fractions: Finding the LCM of the denominators is crucial for adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
-
Scheduling: Consider two events that repeat at different intervals. The LCM helps determine when both events will occur simultaneously. For example, if two buses leave a station at different intervals, the LCM determines when they will leave at the same time again.
-
Modular Arithmetic: In modular arithmetic (working with remainders after division), the LCM plays a vital role in solving congruences and determining periodicity of repeating patterns.
-
Music Theory: The LCM is involved in calculations related to musical intervals and harmonies.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The least common multiple (LCM) is the smallest number divisible by both given numbers. The greatest common divisor (GCD) is the largest number that divides both given numbers without leaving a remainder. They are inversely related, as shown by the formula: LCM(a, b) x GCD(a, b) = a x b
Q2: Can the LCM of two numbers be equal to one of the numbers?
A2: Yes, this happens when one number is a multiple of the other. For example, LCM(6, 12) = 12 because 12 is a multiple of 6.
Q3: Is there a formula for finding the LCM of more than two numbers?
A3: Yes, the prime factorization method extends naturally to multiple numbers. You find the prime factorization of each number, then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to get the LCM.
Conclusion
Finding the least common multiple of 42 and 30, which we found to be 210, demonstrates the importance of understanding fundamental mathematical concepts. We explored three different methods – prime factorization, listing multiples, and using the GCD – each offering a unique perspective on the problem. Understanding these methods not only provides a solution but enhances our comprehension of number theory and its applications in diverse areas, ranging from basic arithmetic to advanced mathematical concepts. The LCM is more than just a simple calculation; it’s a cornerstone of many mathematical operations and a testament to the elegant structure of numbers. Remember to choose the method that best suits the numbers involved; prime factorization is generally the most efficient for larger numbers, while listing multiples can be more intuitive for smaller numbers. The GCD method offers an alternative approach, leveraging the relationship between LCM and GCD to provide a concise solution.
Latest Posts
Latest Posts
-
Weight Of 1 Liter Water
Sep 21, 2025
-
Calories In One Fried Egg
Sep 21, 2025
-
How Tall Is 62 Cm
Sep 21, 2025
-
Prime Factor Tree For 220
Sep 21, 2025
-
7 8ths Of An Inch
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 42 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.