Lcm Of 4 And 10
sportsmenna
Sep 23, 2025 · 6 min read
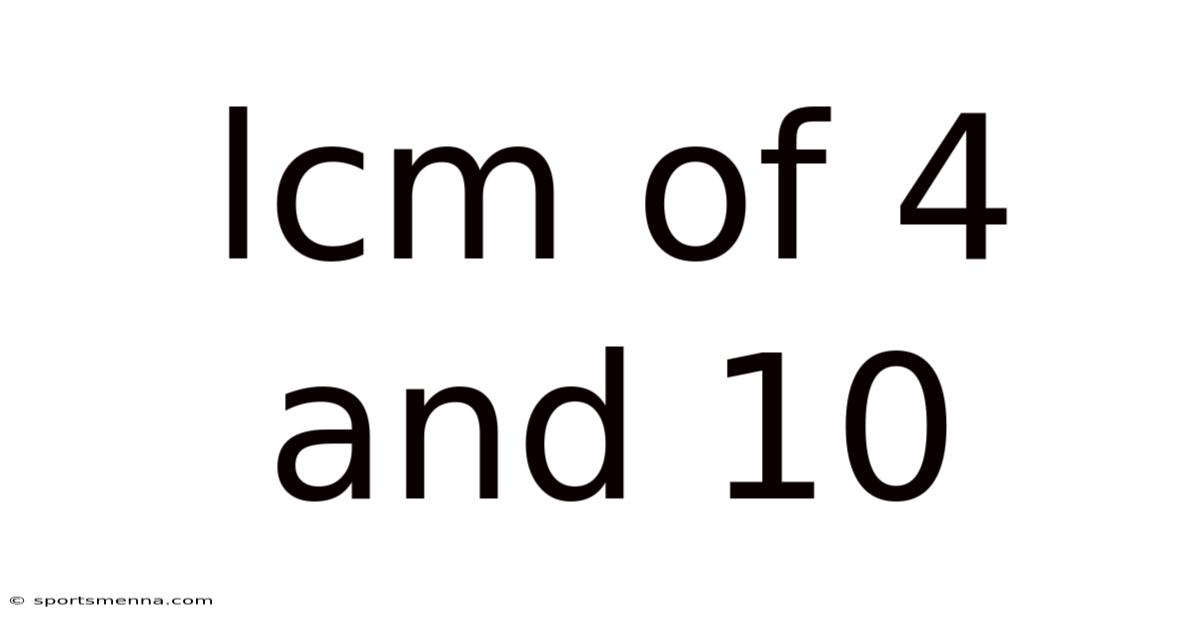
Table of Contents
Unveiling the Least Common Multiple (LCM) of 4 and 10: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation of number theory and its practical applications. This article will delve into the process of calculating the LCM of 4 and 10, exploring various methods, explaining the mathematical principles involved, and offering insights into why this concept is so crucial in various fields. We'll cover everything from basic definitions to advanced techniques, ensuring a comprehensive understanding for readers of all mathematical backgrounds. By the end, you'll not only know the LCM of 4 and 10 but also possess the tools to calculate the LCM of any two (or more) numbers.
Understanding Least Common Multiples (LCM)
Before we tackle the specific example of 4 and 10, let's solidify our understanding of the LCM concept. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly.
For instance, consider the numbers 2 and 3. Multiples of 2 are: 2, 4, 6, 8, 10, 12, 14, 16... Multiples of 3 are: 3, 6, 9, 12, 15, 18... The common multiples are 6, 12, 18... and the least common multiple is 6.
Understanding LCMs is vital in many real-world scenarios. Imagine you have two circular gears with 4 and 10 teeth respectively. The LCM will tell you after how many rotations both gears will return to their starting position simultaneously. This concept is crucial in engineering, scheduling, and various other fields.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to 4 and 10:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 10: 10, 20, 30, 40, 50...
By comparing the two lists, we can see that the smallest number present in both lists is 20. Therefore, the LCM of 4 and 10 is 20.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and elegant method involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Let's find the prime factorization of 4 and 10:
- 4 = 2 x 2 = 2²
- 10 = 2 x 5
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
- The prime factors are 2 and 5.
- The highest power of 2 is 2² = 4.
- The highest power of 5 is 5¹ = 5.
Therefore, the LCM of 4 and 10 is 2² x 5 = 4 x 5 = 20.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 4 and 10 using the Euclidean algorithm:
- Divide the larger number (10) by the smaller number (4): 10 ÷ 4 = 2 with a remainder of 2.
- Replace the larger number with the smaller number (4) and the smaller number with the remainder (2): 4 ÷ 2 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 2. Therefore, GCD(4, 10) = 2.
Now, we can use the formula:
LCM(4, 10) = (4 x 10) / GCD(4, 10) = 40 / 2 = 20
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method offers a powerful and generalizable approach to finding the LCM of any set of numbers. The fundamental theorem of arithmetic states that every integer greater than 1 can be expressed uniquely as a product of prime numbers. This unique representation allows us to systematically find the LCM by considering the highest powers of each prime factor.
This method's strength lies in its ability to handle larger numbers and multiple numbers efficiently. Imagine finding the LCM of 12, 18, and 30 using the listing method; it would be quite tedious. However, using prime factorization:
- 12 = 2² x 3
- 18 = 2 x 3²
- 30 = 2 x 3 x 5
The highest power of 2 is 2², the highest power of 3 is 3², and the highest power of 5 is 5. Therefore, LCM(12, 18, 30) = 2² x 3² x 5 = 4 x 9 x 5 = 180.
Applications of LCM in Real-World Problems
The concept of LCM extends beyond simple arithmetic exercises. Its applications are widespread and crucial in numerous fields:
- Scheduling: Imagine two buses leaving a station at different intervals. The LCM of their intervals will determine when they depart together again.
- Engineering: In gear systems, as mentioned earlier, the LCM helps determine when gears will return to their initial positions simultaneously.
- Music: LCMs are used in music theory to find the least common multiple of different note durations, which is crucial for composing and harmonizing music.
- Project Management: If tasks repeat at different intervals, LCM helps determine when all tasks will coincide, aiding in project scheduling and resource allocation.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both numbers evenly. They are inversely related.
Q: Can the LCM of two numbers be greater than the product of the two numbers?
A: No, the LCM of two numbers is always less than or equal to the product of the two numbers.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method to include all numbers. Find the prime factorization of each number, then take the highest power of each prime factor present across all factorizations and multiply them together.
Q: Is there a formula for calculating the LCM of any two numbers?
A: Yes, the formula is LCM(a, b) = (a x b) / GCD(a, b), where GCD is the greatest common divisor.
Q: Why is understanding LCM important?
A: Understanding LCM is crucial for solving various real-world problems involving cycles, repetitions, and synchronization, as seen in scheduling, engineering, and music.
Conclusion
The LCM of 4 and 10, as demonstrated through various methods, is 20. However, the true value of this exercise lies not just in the answer but in understanding the underlying principles of number theory, prime factorization, and the relationship between LCM and GCD. These concepts are foundational to more advanced mathematical topics and possess practical applications across various disciplines. By mastering these techniques, you'll equip yourself with valuable problem-solving skills applicable far beyond the realm of simple arithmetic. The ability to efficiently calculate LCMs is a testament to a deeper grasp of number theory and its practical significance in our world.
Latest Posts
Latest Posts
-
Xmas Words Starting With Q
Sep 23, 2025
-
How Many Prophets Of Allah
Sep 23, 2025
-
Cast Of The Sparticle Mystery
Sep 23, 2025
-
Beverages That Start With G
Sep 23, 2025
-
Lcm Of 6 2 5
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.