Lcm Of 6 2 5
sportsmenna
Sep 23, 2025 · 6 min read
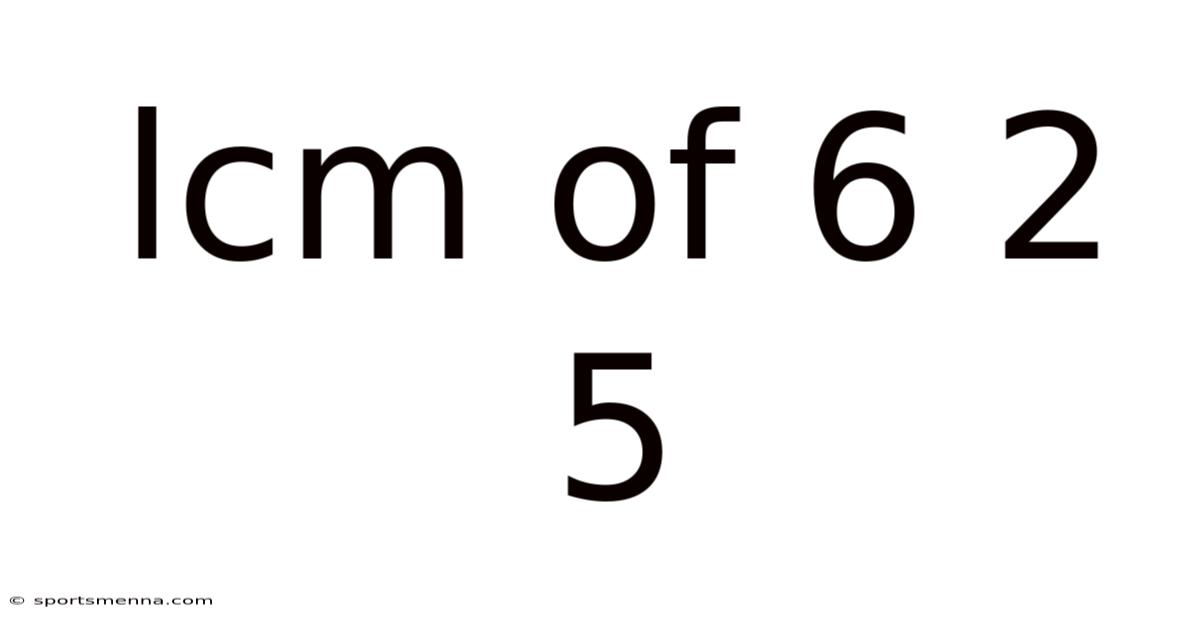
Table of Contents
Understanding the Least Common Multiple (LCM): A Deep Dive into Finding the LCM of 6, 2, and 5
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 6, 2, and 5. However, understanding the underlying concepts and different methods for calculating the LCM provides a solid foundation for more complex mathematical problems. This article will guide you through various approaches to find the LCM of 6, 2, and 5, explaining the process step-by-step and delving into the theoretical basis of the LCM. We'll explore different methods, suitable for various levels of mathematical understanding, from elementary school to more advanced levels. By the end of this article, you'll not only know the LCM of 6, 2, and 5 but also possess a comprehensive understanding of LCM calculations and their applications.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding this definition is crucial before we tackle the specific problem of finding the LCM of 6, 2, and 5. The LCM is a fundamental concept in mathematics, with applications extending to various fields, including fractions, scheduling, and even music theory.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, ...
By examining the lists, we can see that the smallest number common to all three lists is 30. Therefore, the LCM of 6, 2, and 5 is 30. This method is excellent for visualizing the concept of the LCM but can become cumbersome when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors. Prime factors are prime numbers that, when multiplied together, equal the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 2: 2
- Prime Factorization of 5: 5
Next, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, we multiply these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM of 6, 2, and 5 is 30. This method is generally more efficient and less prone to errors than the listing method, particularly when dealing with larger numbers or a greater number of integers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
There's a useful relationship between the LCM and the greatest common divisor (GCD) of two numbers:
LCM(a, b) * GCD(a, b) = a * b
While this formula directly applies to only two numbers, we can extend it to find the LCM of multiple numbers by applying it iteratively. First, let's find the GCD of 6 and 2 using the Euclidean Algorithm.
- Divide 6 by 2: 6 = 2 * 3 + 0. The remainder is 0, so the GCD(6, 2) is 2.
Now, we can use the formula:
LCM(6, 2) * GCD(6, 2) = 6 * 2 LCM(6, 2) * 2 = 12 LCM(6, 2) = 6
Now, let's find the LCM of 6 and 5. The GCD(6,5) is 1 (as 6 and 5 share no common factors other than 1).
LCM(6, 5) * GCD(6, 5) = 6 * 5 LCM(6, 5) * 1 = 30 LCM(6, 5) = 30
Finally, we need to find the LCM of the result (30) and the remaining number (2). The GCD(30,2) is 2.
LCM(30,2) * GCD(30,2) = 30 * 2 LCM(30,2) * 2 = 60 LCM(30,2) = 30
Thus, even using the iterative GCD approach, the LCM of 6, 2, and 5 is 30. This method might seem more complex initially, but it illustrates a crucial relationship between LCM and GCD, which is valuable for more advanced mathematical concepts.
Method 4: Using the Least Common Multiple Calculator (For Verification)
While not a manual method, using an online LCM calculator can serve as a valuable tool for verification. Inputting the numbers 6, 2, and 5 into a reliable calculator will confirm our result of 30. This isn't a primary method for understanding the why behind the LCM, but it's helpful for double-checking your calculations, especially with more complex sets of numbers.
Applications of LCM
The LCM has several practical applications in various fields:
- Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions. This allows you to find a common denominator, simplifying the calculation.
- Scheduling: Determining when events will occur simultaneously, such as the timing of bus schedules or the overlapping of work shifts, often involves using the LCM. For example, if one bus arrives every 6 minutes and another every 2 minutes, the LCM (6, 2) = 6 tells us they both arrive at the same time every 6 minutes.
- Music Theory: The LCM plays a role in music theory, particularly in determining the least common denominator for rhythmic patterns or determining when different musical phrases will align.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have a common factor greater than 1?
- A: The methods discussed above, particularly prime factorization, will automatically account for common factors. The highest power of each prime factor will be used, ensuring the correct LCM.
-
Q: Can the LCM of three or more numbers be 1?
- A: No, the LCM of two or more integers is always greater than or equal to the largest of the integers. The only way the LCM could be 1 is if all the numbers themselves are 1.
-
Q: Is there a formula for finding the LCM of more than two numbers?
- A: While there isn't a single, compact formula for multiple numbers like the GCD/LCM relationship for two numbers, the prime factorization method is the most straightforward and widely applicable approach.
Conclusion
Finding the least common multiple of 6, 2, and 5, while seemingly simple, opens a window into a significant mathematical concept with diverse applications. We've explored several methods – listing multiples, prime factorization, and the GCD/LCM relationship – each providing a different perspective on calculating the LCM. Understanding these methods not only equips you to solve similar problems but also enhances your grasp of fundamental mathematical principles. Remember that choosing the most appropriate method depends on the numbers involved and your level of mathematical comfort. The prime factorization method is generally recommended for its efficiency and conceptual clarity, especially as the numbers become larger and more complex. The LCM, like many mathematical concepts, isn't just about finding the answer but also about appreciating the underlying logic and its real-world relevance.
Latest Posts
Latest Posts
-
How Long Is 2 Miles
Sep 23, 2025
-
Occupations That Start With Y
Sep 23, 2025
-
Saying One Thing Doing Another
Sep 23, 2025
-
Xmas Words Starting With Q
Sep 23, 2025
-
How Many Prophets Of Allah
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.