Lcm Of 3 7 2
sportsmenna
Sep 22, 2025 · 5 min read
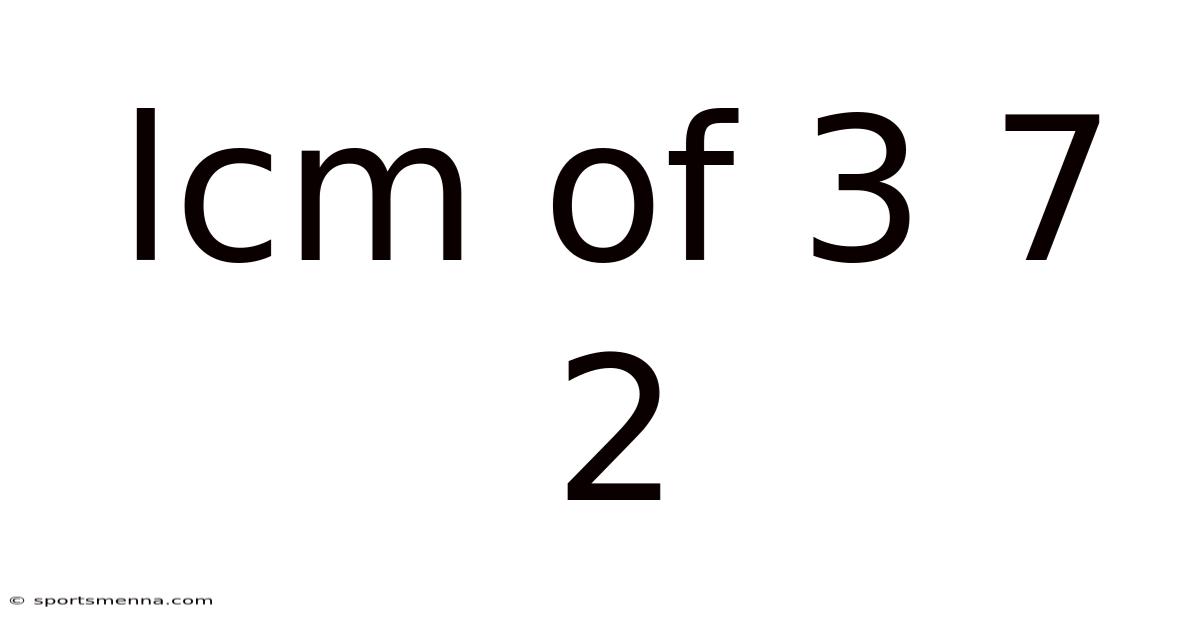
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 7, and 2: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even real-world applications involving cycles and timing. This article will provide a comprehensive understanding of how to calculate the LCM of 3, 7, and 2, explaining different methods and delving into the underlying mathematical principles. We'll also explore why understanding LCM is so important and answer frequently asked questions. By the end, you'll be confident in calculating LCMs not just for these three numbers but for any set of integers.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding LCM is essential for various mathematical operations, including adding and subtracting fractions with different denominators.
Let's consider our example: finding the LCM of 3, 7, and 2. This means we're looking for the smallest positive integer that is divisible by 3, 7, and 2 without leaving a remainder.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, involves listing the multiples of each number until we find a common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36, 42...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42...
By comparing the lists, we can see that the smallest number that appears in all three lists is 42. Therefore, the LCM of 3, 7, and 2 is 42. This method is easy to visualize but can become cumbersome with larger numbers.
Method 2: Prime Factorization
A more efficient method, particularly for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization:
- 3 = 3 (3 is a prime number)
- 7 = 7 (7 is a prime number)
- 2 = 2 (2 is a prime number)
-
Identifying the Highest Power of Each Prime Factor: We look at the prime factors from each number and take the highest power of each. In this case, we have:
- 2¹
- 3¹
- 7¹
-
Multiplying the Highest Powers: To find the LCM, we multiply these highest powers together: 2¹ * 3¹ * 7¹ = 42
Therefore, the LCM of 3, 7, and 2 is 42, confirming our result from the previous method. This method is significantly more efficient for larger numbers and sets of numbers because it avoids the tedious process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a formula that connects the LCM and GCD:
LCM(a, b, c) * GCD(a, b, c) = a * b * c
While this formula works for two numbers easily, applying it directly to three or more numbers is less straightforward. It's generally more efficient to use prime factorization to find both the LCM and GCD.
Let's illustrate this for our numbers:
-
Finding the GCD: Since 3, 7, and 2 are all prime numbers and don't share any common factors other than 1, their GCD is 1.
-
Applying the Formula (Approximation for Multiple Numbers): While the formula isn't directly applicable in its simplest form to three or more numbers, we can adapt it. We know that LCM(3, 7, 2) * GCD(3, 7, 2) should roughly equal 3 * 7 * 2 = 42. Since GCD(3, 7, 2) = 1, this suggests LCM(3, 7, 2) = 42. This method helps understand the relationship but isn't the most reliable calculation method for multiple numbers.
Why is Understanding LCM Important?
The concept of LCM has wide-ranging applications in various fields:
-
Fraction Operations: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation. For example, to add 1/3 + 1/7 + 1/2, we need to find the LCM of 3, 7, and 2, which is 42. This allows us to rewrite the fractions with a common denominator and easily add them.
-
Scheduling and Cycles: LCM is used to solve problems involving recurring events or cycles. For instance, if three different machines complete their cycles in 3, 7, and 2 hours respectively, the LCM (42 hours) determines when they will all complete a cycle simultaneously.
-
Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory used in cryptography and computer science.
-
Measurement Conversions: In various measurement conversions, LCM can help in finding the least common multiple of different units.
Frequently Asked Questions (FAQ)
-
What if the numbers share common factors? The prime factorization method handles this effortlessly. The highest power of each prime factor will be considered, regardless of whether it appears in multiple numbers.
-
Can I use a calculator to find the LCM? Many scientific calculators have built-in functions to calculate the LCM of multiple numbers. However, understanding the underlying methods is crucial for a deeper mathematical understanding.
-
What if one of the numbers is zero? The LCM of any set of numbers containing zero is undefined because zero is a multiple of every number.
-
Is there a formula for finding the LCM of more than two numbers directly? While there isn't a single, concise formula like the one for two numbers, the prime factorization method works efficiently for any number of integers.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with practical applications in various fields. While listing multiples can be a starting point for smaller numbers, prime factorization offers a far more efficient and reliable approach for larger numbers and multiple integers. Understanding the methods and the relationship between LCM and GCD empowers you to tackle mathematical problems effectively and appreciate the broader applications of this vital concept. Remember, the LCM of 3, 7, and 2, calculated using any of the methods discussed above, is 42. Now you have the tools and knowledge to confidently calculate the LCM of any set of integers you encounter.
Latest Posts
Latest Posts
-
Why Are Scots Called Jocks
Sep 22, 2025
-
63 Kg How Many Pounds
Sep 22, 2025
-
What Is 70mm In Inches
Sep 22, 2025
-
What Is 25 Of 10
Sep 22, 2025
-
Area Code For Cardiff Uk
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 7 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.