Lcm Of 130 And 165
sportsmenna
Sep 19, 2025 · 6 min read
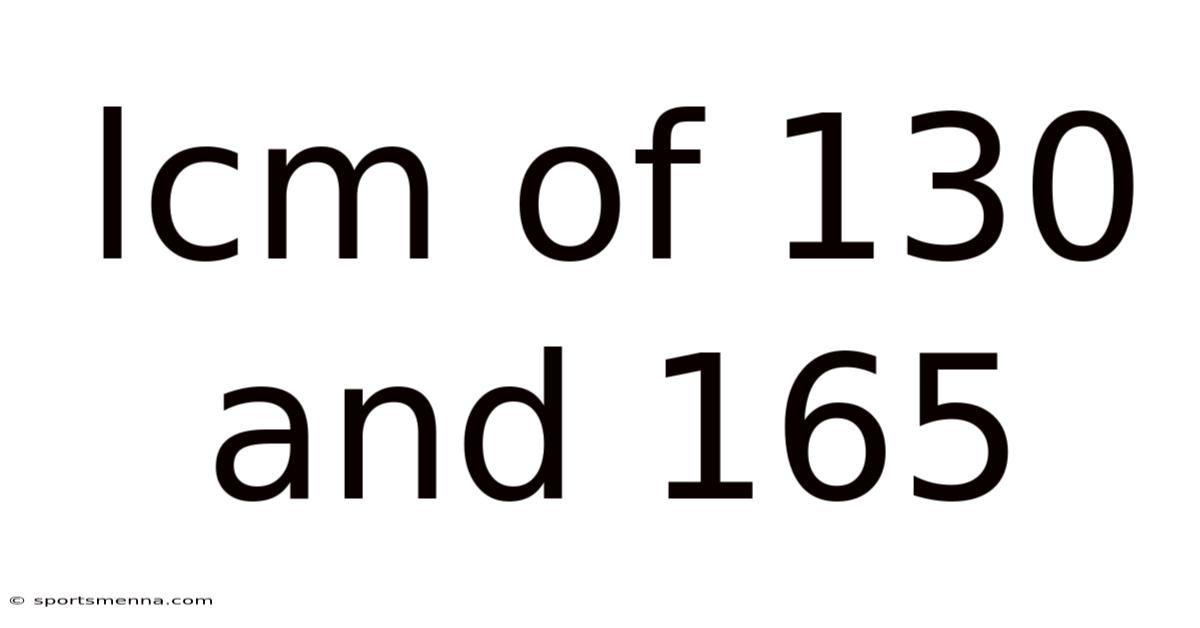
Table of Contents
Finding the Least Common Multiple (LCM) of 130 and 165: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and different methods for calculating it can be surprisingly insightful. This article delves deep into finding the LCM of 130 and 165, exploring multiple approaches – from prime factorization to the Euclidean algorithm – to provide a thorough understanding of this fundamental concept in number theory. We'll also explore the practical applications of LCMs and address common questions.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. Understanding LCMs is crucial in various mathematical applications, including solving problems involving fractions, scheduling events, and working with rhythmic patterns. This article focuses on finding the LCM of 130 and 165, illustrating several methods along the way.
Method 1: Prime Factorization
This is perhaps the most straightforward method for calculating the LCM, especially for smaller numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Find the prime factorization of 130.
130 can be factored as 2 x 5 x 13. This means 130 = 2¹ x 5¹ x 13¹.
Step 2: Find the prime factorization of 165.
165 can be factored as 3 x 5 x 11. This means 165 = 3¹ x 5¹ x 11¹.
Step 3: Identify the highest power of each prime factor.
Comparing the prime factorizations of 130 and 165, we have the following prime factors: 2, 3, 5, 11, and 13. The highest power of each is:
- 2¹
- 3¹
- 5¹
- 11¹
- 13¹
Step 4: Multiply the highest powers together.
To find the LCM, we multiply the highest powers of each prime factor together:
LCM(130, 165) = 2¹ x 3¹ x 5¹ x 11¹ x 13¹ = 2 x 3 x 5 x 11 x 13 = 4290
Therefore, the least common multiple of 130 and 165 is 4290.
Method 2: Listing Multiples
This method is more intuitive but can be less efficient for larger numbers. It involves listing the multiples of each number until a common multiple is found.
Step 1: List multiples of 130.
Multiples of 130: 130, 260, 390, 520, 650, 780, 910, 1040, 1170, 1300, 1430, 1560, 1690, 1820, 1950, 2080, 2210, 2340, 2470, 2600, 2730, 2860, 2990, 3120, 3250, 3380, 3510, 3640, 3770, 3900, 4030, 4160, 4290…
Step 2: List multiples of 165.
Multiples of 165: 165, 330, 495, 660, 825, 990, 1155, 1320, 1485, 1650, 1815, 1980, 2145, 2310, 2475, 2640, 2805, 2970, 3135, 3300, 3465, 3630, 3795, 3960, 4125, 4290…
Step 3: Identify the smallest common multiple.
By comparing the lists, we can see that the smallest common multiple of 130 and 165 is 4290. While this method works, it becomes cumbersome for larger numbers.
Method 3: Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the Euclidean algorithm to find the GCD.
Step 1: Find the GCD of 130 and 165 using the Euclidean algorithm.
- Divide 165 by 130: 165 = 1 x 130 + 35
- Divide 130 by 35: 130 = 3 x 35 + 25
- Divide 35 by 25: 35 = 1 x 25 + 10
- Divide 25 by 10: 25 = 2 x 10 + 5
- Divide 10 by 5: 10 = 2 x 5 + 0
The last non-zero remainder is 5, so the GCD(130, 165) = 5.
Step 2: Apply the formula.
LCM(130, 165) = (130 x 165) / GCD(130, 165) = (21450) / 5 = 4290
This method provides a more efficient approach, especially for larger numbers where listing multiples becomes impractical.
The Euclidean Algorithm Explained
The Euclidean algorithm is a highly efficient method for finding the greatest common divisor (GCD) of two integers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the remainder is zero. The last non-zero remainder is the GCD. Its elegance lies in its iterative nature and its ability to handle even very large numbers effectively.
Practical Applications of LCM
Least common multiples have numerous practical applications across various fields:
-
Scheduling: Imagine two events occurring at different intervals. Finding the LCM helps determine when both events will coincide again. For example, if one event happens every 130 days and another every 165 days, they will coincide again after 4290 days.
-
Fractions: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator.
-
Rhythms and Music: LCM plays a vital role in music theory, helping determine when different rhythmic patterns will synchronize.
-
Gear Ratios: In mechanical engineering, LCM is used in calculating gear ratios to optimize the speed and torque of machinery.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
The least common multiple (LCM) is the smallest number divisible by both numbers, while the greatest common divisor (GCD) is the largest number that divides both numbers without a remainder. They are inversely related; a larger GCD implies a smaller LCM, and vice versa.
Q2: Can the LCM of two numbers be smaller than the larger number?
No. The LCM of two numbers will always be greater than or equal to the larger of the two numbers.
Q3: Is there a limit to the size of numbers for which we can find the LCM?
Theoretically, no. Algorithms like the Euclidean algorithm can handle arbitrarily large numbers, although computational limitations might become a factor for extremely large numbers.
Q4: What if I have more than two numbers? How do I find their LCM?
You can extend the prime factorization method or use iterative applications of the GCD-based formula to find the LCM of more than two numbers. For example, to find the LCM of a, b, and c, you would first find LCM(a, b), and then find the LCM of that result and c.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a fundamental skill in mathematics with wide-ranging applications. This article explored three different methods – prime factorization, listing multiples, and using the GCD – for calculating the LCM of 130 and 165. Understanding these methods, especially the prime factorization and GCD-based approaches, provides a robust foundation for tackling more complex problems involving LCMs. Remember that choosing the most efficient method depends on the context and the size of the numbers involved. The Euclidean algorithm, particularly, provides a powerful and efficient tool for calculating GCDs, which is crucial in the efficient calculation of LCMs. The more you practice these techniques, the more intuitive and efficient you'll become at finding the LCM of any set of numbers.
Latest Posts
Latest Posts
-
13 Degree C To F
Sep 19, 2025
-
Group Of Cattle Is Called
Sep 19, 2025
-
Formula For Iron Iii Chloride
Sep 19, 2025
-
Starter Pokemon In Soul Silver
Sep 19, 2025
-
Does Gas Float On Diesel
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 130 And 165 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.