8 Divided By 1 3
sportsmenna
Sep 22, 2025 · 6 min read
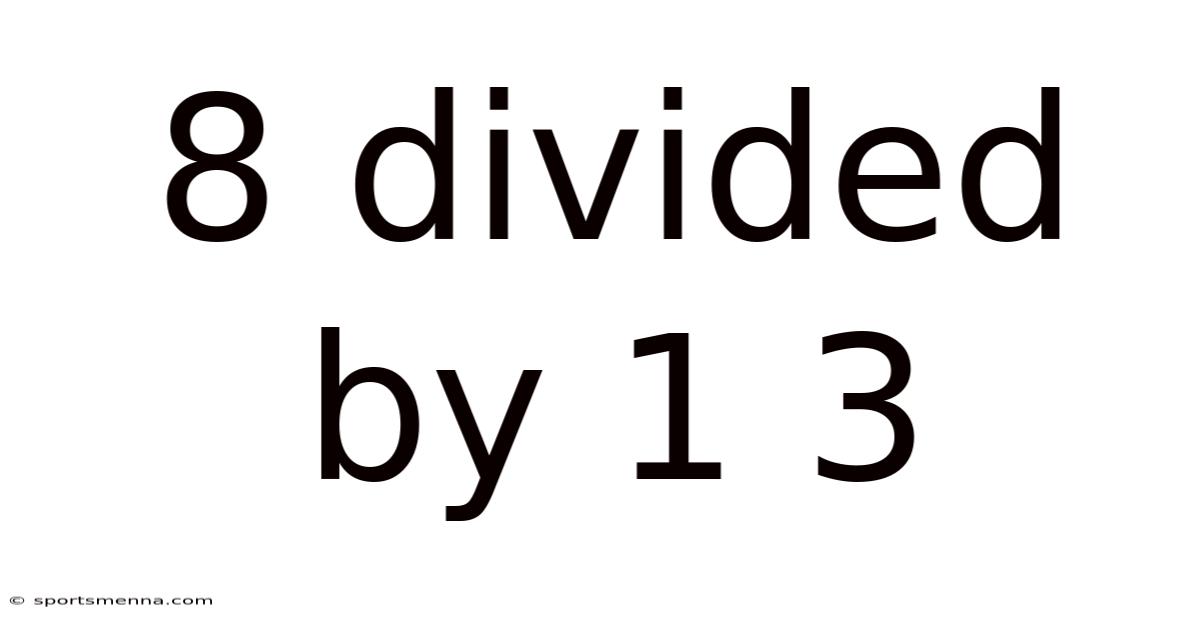
Table of Contents
Diving Deep into Division: Understanding 8 Divided by 1/3
Many find fractions daunting, and division involving fractions can seem especially tricky. This comprehensive guide will demystify the process of dividing 8 by 1/3, explaining not only the solution but also the underlying mathematical principles. We'll explore different approaches, address common misconceptions, and equip you with the confidence to tackle similar problems. Understanding this seemingly simple problem unlocks a deeper understanding of fraction division, a crucial skill in various fields, from baking to engineering.
Introduction: Why is 8 ÷ 1/3 a Challenging Concept?
The core difficulty lies in understanding what division actually represents. When we say "8 divided by 2," we're asking: "How many times does 2 fit into 8?" The answer, of course, is 4. But when we introduce fractions, the visual representation becomes less intuitive. Dividing by a fraction like 1/3 is akin to asking: "How many one-thirds are there in 8?" This requires a shift in perspective from whole numbers to parts of a whole.
Method 1: The "Keep, Change, Flip" Method (aka. Reciprocal Method)
This is perhaps the most widely known method for dividing fractions. It's a shortcut based on the mathematical properties of fractions and division. Here's how it works:
- Keep: Keep the first number (the dividend) as it is: 8.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of 1/3 is 3/1 (or simply 3).
So, 8 ÷ 1/3 becomes 8 × 3. This simplifies to 24.
Explanation: Why does "keep, change, flip" work? It's based on the understanding that dividing by a fraction is the same as multiplying by its reciprocal. Mathematically, this is proven through the properties of fractions and multiplicative inverses.
Method 2: The Visual Approach – Using Diagrams
Visualizing the problem can be incredibly helpful, particularly for those who struggle with abstract mathematical concepts. Imagine a whole divided into thirds.
- We have 8 wholes.
- Each whole contains 3 thirds (3/3 = 1).
- Therefore, the total number of thirds in 8 wholes is 8 × 3 = 24.
This visual method makes the concept more concrete and easier to grasp. You can draw diagrams representing the wholes and their thirds to physically demonstrate the calculation. This method is particularly useful for beginners and for reinforcing the understanding of fractions.
Method 3: Using the Definition of Division
We can also approach this problem by considering the definition of division itself. Division asks: "How many groups of a certain size can we make from a larger quantity?"
In this case:
- We have a total quantity of 8.
- We want to find out how many groups of size 1/3 we can make.
To find out, we need to determine how many 1/3s are in 8. This is equivalent to asking 8 ÷ (1/3) = ? This leads us back to the concept of reciprocals and the "keep, change, flip" method. We essentially multiply 8 by 3 to find the total number of thirds.
Method 4: Converting to Improper Fractions
This method involves converting the whole number into a fraction, making the division process more straightforward.
- Represent 8 as a fraction: 8/1.
- Now, the problem becomes (8/1) ÷ (1/3).
- To divide fractions, we multiply the first fraction by the reciprocal of the second fraction: (8/1) × (3/1).
- This simplifies to 24/1, or 24.
Addressing Common Misconceptions:
-
Confusing multiplication with division: Some students mistakenly multiply 8 and 1/3 instead of dividing. Remember that dividing by a fraction increases the result, not decreases it. Think about it: you can fit more smaller pieces (thirds) into a larger whole (8) than you can fit larger pieces (whole numbers).
-
Incorrectly inverting the wrong fraction: Only the divisor (the number you're dividing by) is inverted (reciprocated). The dividend (the number being divided) stays the same.
-
Failing to simplify: After completing the calculation, always simplify your answer if possible. In this case, 24 is already in its simplest form.
Understanding the Concept of Reciprocals
The reciprocal of a number is the number that, when multiplied by the original number, results in 1. For example:
- The reciprocal of 2 is 1/2 (because 2 × 1/2 = 1).
- The reciprocal of 1/3 is 3 (because 1/3 × 3 = 1).
- The reciprocal of 5/7 is 7/5 (because 5/7 × 7/5 = 1).
Understanding reciprocals is fundamental to mastering fraction division.
Real-World Applications:
Division involving fractions isn't just an abstract mathematical exercise; it has numerous real-world applications:
-
Baking: A recipe calls for 1/3 cup of sugar per serving. If you want to make 8 servings, you'll need 8 ÷ 1/3 = 24/3 = 8 cups of sugar.
-
Construction: If a piece of wood is 8 meters long, and each section needs to be 1/3 meter long, how many sections can be cut from it? The answer, 24, is vital for efficient planning.
-
Sewing/Tailoring: Determining the number of smaller pieces that can be cut from a larger piece of fabric.
-
Engineering: Calculating the number of smaller components needed to build a larger structure.
Frequently Asked Questions (FAQs):
-
Q: What if the dividend (the number being divided) was a fraction as well? A: The "keep, change, flip" method still applies. You would keep the first fraction, change the division sign to multiplication, and flip the second fraction. Then, you would multiply the numerators and the denominators. Remember to simplify the result if necessary.
-
Q: Can I use a calculator to solve this? A: Yes, most calculators can handle fraction division. However, understanding the underlying mathematical principles is crucial for problem-solving and developing a deeper understanding of mathematics.
-
Q: Why is this concept important? A: Mastering fraction division is essential for higher-level mathematics, science, and engineering. It builds a strong foundation in numerical reasoning and problem-solving skills.
Conclusion: Mastering Fraction Division
Dividing 8 by 1/3 might seem initially intimidating, but with a clear understanding of the principles of fraction division and the various methods available, it becomes a manageable and even enjoyable task. Whether you prefer the visual approach, the "keep, change, flip" method, or converting to improper fractions, the key lies in breaking down the problem into smaller, more understandable steps. By practicing these methods and grasping the underlying concepts, you'll not only solve this specific problem but gain the confidence to tackle more complex fraction division problems in the future. Remember that consistent practice and a willingness to explore different approaches are key to mastering any mathematical concept. Embrace the challenge, and you will find that the seemingly complex world of fractions can become clear and even fascinating.
Latest Posts
Latest Posts
-
Calories In Weetabix With Milk
Sep 22, 2025
-
Christmas Words Beginning With Y
Sep 22, 2025
-
Penultimate Letter In Greek Alphabet
Sep 22, 2025
-
What Is 40 Of 50
Sep 22, 2025
-
Jo Brand And John Sergeant
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.