What Is 40 Of 50
sportsmenna
Sep 22, 2025 · 6 min read
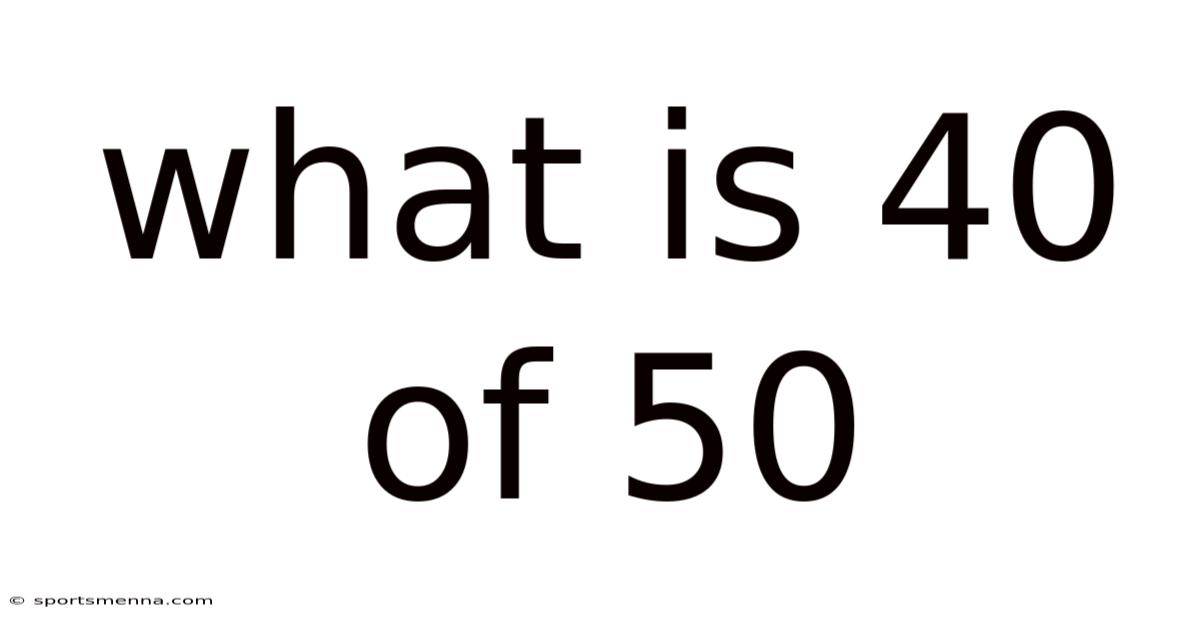
Table of Contents
What is 40 of 50? Understanding Percentages and Fractions
This article delves into the seemingly simple question: "What is 40 of 50?" While the answer might seem immediately obvious to some, this question provides a fantastic springboard to explore fundamental mathematical concepts like fractions, percentages, ratios, and their practical applications. We'll unpack the calculation, explore different approaches to solving it, and examine its relevance in various real-world scenarios. Understanding this seemingly simple calculation will build a solid foundation for more complex mathematical problems.
Understanding the Question
The phrase "40 of 50" inherently represents a part-to-whole relationship. It asks us to determine what proportion 40 represents when compared to the total of 50. This type of problem can be solved using several methods, each providing a different perspective and enhancing your understanding of mathematical principles.
Method 1: Converting to a Fraction
The most straightforward approach is to express the relationship as a fraction. The number 40 represents the part, and 50 represents the whole. Therefore, the fraction is written as 40/50.
This fraction can then be simplified by finding the greatest common divisor (GCD) of 40 and 50. The GCD of 40 and 50 is 10. Dividing both the numerator (40) and the denominator (50) by 10 gives us the simplified fraction 4/5.
This simplified fraction, 4/5, represents the proportion of 40 out of 50. It tells us that 40 is four-fifths of 50.
Method 2: Calculating the Percentage
Converting the fraction to a percentage offers another perspective. To do this, we take the fraction 40/50 (or the simplified fraction 4/5) and multiply it by 100%:
(40/50) * 100% = 80%
Therefore, 40 is 80% of 50. This percentage representation is extremely useful for expressing proportions in various contexts, from financial reports to scientific data analysis.
Method 3: Using Decimal Representation
Alternatively, we can express the fraction 40/50 as a decimal. Dividing 40 by 50 gives us:
40 ÷ 50 = 0.8
This decimal, 0.8, is equivalent to both the fraction 4/5 and the percentage 80%. Decimal representation is frequently used in calculations involving computers and scientific applications.
Method 4: Understanding Ratios
The relationship between 40 and 50 can also be expressed as a ratio. A ratio is a comparison of two or more quantities. In this case, the ratio is 40:50. Like the fraction, this ratio can be simplified by dividing both numbers by their GCD (10), resulting in the simplified ratio 4:5. This ratio signifies that for every 4 parts, there are 5 parts in total.
Real-World Applications
Understanding how to calculate "40 of 50" has practical applications across numerous fields:
- Finance: Imagine you invested $50 and earned a profit of $40. Calculating the percentage return (80%) is crucial for evaluating investment performance.
- Sales: If a company aimed to sell 50 units and sold 40, understanding the 80% sales achievement helps analyze sales performance and identify areas for improvement.
- Education: If a student answered 40 questions correctly out of 50, the 80% score reflects their understanding of the subject matter.
- Science: In scientific experiments, calculating percentages or ratios from data is essential for analyzing results and drawing meaningful conclusions. For example, if a scientist observes 40 successful trials out of 50 attempts, the 80% success rate informs further research.
- Everyday Life: Many everyday tasks involve calculating percentages or fractions. For example, determining the discount on a sale item, calculating the tip at a restaurant, or dividing a recipe.
Expanding the Concept: Proportions and Variations
The concept of "40 of 50" expands beyond a simple calculation. It introduces the fundamental concept of proportions. A proportion is a statement that two ratios are equal. We can use proportions to solve problems where we know a part and the whole, and need to find a corresponding part for a different whole.
For example:
If 40 is 80% of 50, what is 80% of 100?
We can set up a proportion:
40/50 = x/100
Solving for x (by cross-multiplying):
50x = 4000 x = 80
Therefore, 80 is 80% of 100. This illustrates the power of understanding proportions in solving various related problems.
Dealing with More Complex Scenarios
While "40 of 50" is a relatively straightforward calculation, the underlying principles apply to more complex situations. Imagine a scenario where you need to calculate a percentage from a larger dataset or a problem involving multiple variables.
For example, let’s say you have a dataset of 500 items, and 200 of them are defective. To find the percentage of defective items:
(200/500) * 100% = 40%
This illustrates that the core principle remains the same, even with larger numbers. The ability to break down complex problems into smaller, manageable steps—like converting to fractions, decimals, or percentages—is a valuable problem-solving skill.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 40/50?
A: The simplest form of 40/50 is 4/5. This is obtained by dividing both the numerator and denominator by their greatest common divisor, which is 10.
Q: Can I use a calculator to solve this problem?
A: Absolutely! A calculator can quickly convert fractions to decimals and percentages. However, understanding the underlying mathematical principles is crucial for developing problem-solving skills beyond simple calculations.
Q: What if the numbers are not as easily divisible?
A: Even with larger or less easily divisible numbers, the same principles apply. You can always use a calculator to find the decimal representation and then multiply by 100% to find the percentage. Simplifying fractions might require finding the greatest common divisor, which can be done through prime factorization or using the Euclidean algorithm.
Q: Are there other ways to represent 40 out of 50?
A: Yes, besides fractions, percentages, and decimals, you can represent it as a ratio (40:50 or simplified to 4:5) or even graphically using a pie chart or bar graph.
Conclusion
The seemingly simple question, "What is 40 of 50?", opens up a broad understanding of fundamental mathematical concepts. By approaching this problem through fractions, percentages, decimals, and ratios, we've explored a range of mathematical tools and their real-world applications. Mastering these core concepts provides a strong foundation for tackling more advanced mathematical problems and enhances analytical skills applicable across various disciplines. Remember, the key lies not only in finding the answer (80%) but also in understanding the why behind the calculation and the various ways to represent the same relationship. This deeper understanding empowers you to tackle complex problems with confidence and efficiency.
Latest Posts
Latest Posts
-
2 Weetabix And Milk Calories
Sep 22, 2025
-
What Does Allah Hafiz Mean
Sep 22, 2025
-
Weight Of 1 Litre Water
Sep 22, 2025
-
Jobs That Start With Y
Sep 22, 2025
-
Items That Start With V
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.