6 30 As A Percent
sportsmenna
Sep 23, 2025 · 5 min read
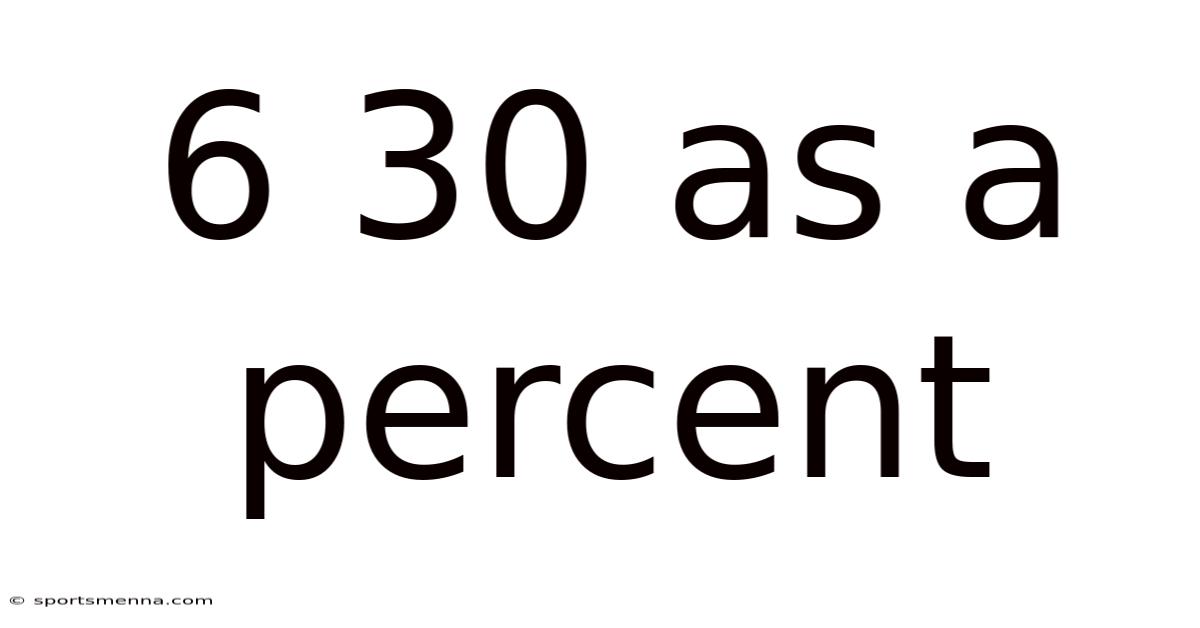
Table of Contents
6:30 as a Percent: Understanding Ratios and Conversions
Understanding how to represent ratios as percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday life calculations. This article will delve into the process of converting the ratio 6:30 into a percentage, providing a step-by-step guide, exploring the underlying concepts, and answering frequently asked questions. We'll go beyond a simple answer, equipping you with a thorough understanding of ratio and percentage conversions.
Introduction: Deconstructing the Ratio
The ratio 6:30 represents a relationship between two numbers, 6 and 30. It signifies that for every 6 units of one quantity, there are 30 units of another. To express this relationship as a percentage, we need to determine what portion of the whole 30 units is represented by the 6 units. Essentially, we are asking: "6 is what percent of 30?"
Step-by-Step Conversion: From Ratio to Percentage
Here's a breakdown of how to convert the ratio 6:30 into a percentage:
-
Find the Total: The first step is to find the total number of units. In our ratio, the total is 6 + 30 = 36 units.
-
Calculate the Fraction: Next, express the first number in the ratio (6) as a fraction of the total (36). This gives us the fraction 6/36.
-
Simplify the Fraction (Optional but Recommended): Simplifying fractions makes the next step easier. We can divide both the numerator (6) and the denominator (36) by their greatest common divisor, which is 6. This simplifies the fraction to 1/6.
-
Convert the Fraction to a Decimal: To convert the fraction to a decimal, divide the numerator by the denominator: 1 ÷ 6 = 0.166666... (This is a repeating decimal).
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 to express it as a percentage: 0.166666... × 100 = 16.67% (rounded to two decimal places).
Therefore, 6:30 as a percentage is approximately 16.67%.
Understanding the Underlying Concepts
Let's delve deeper into the mathematical principles behind this conversion:
-
Ratios: A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. Ratios can be expressed in different forms: using a colon (e.g., 6:30), as a fraction (e.g., 6/30), or in words (e.g., "6 to 30").
-
Fractions: A fraction represents a part of a whole. The numerator (top number) represents the part, and the denominator (bottom number) represents the whole.
-
Decimals: Decimals are another way of representing fractions. They use a base-10 system, with the decimal point separating the whole number part from the fractional part.
-
Percentages: A percentage is a way of expressing a fraction or decimal as a proportion of 100. The percentage symbol (%) represents "per hundred". To convert a decimal to a percentage, you multiply by 100 and add the % symbol.
Real-World Applications: Where This Conversion is Useful
The ability to convert ratios to percentages is vital in various real-world scenarios:
-
Finance: Calculating interest rates, profit margins, and investment returns often involves converting ratios to percentages. For instance, if a company makes a profit of $6 out of a total revenue of $30, its profit margin is 16.67%.
-
Statistics: Percentages are used extensively in statistics to represent proportions, probabilities, and changes over time. For example, if a survey shows 6 out of 30 people prefer a particular product, the percentage of people preferring that product is 16.67%.
-
Everyday Life: Many everyday situations require converting ratios to percentages. For example, calculating discounts, calculating the percentage of ingredients in a recipe, or figuring out the percentage of tasks completed in a project.
More Complex Ratio Conversions: Expanding Your Skillset
The principles discussed above can be applied to convert any ratio to a percentage. Let's look at a slightly more complex example: Suppose we have a ratio of 15:45.
-
Total: 15 + 45 = 60
-
Fraction: 15/60
-
Simplification: 15/60 simplifies to 1/4
-
Decimal: 1 ÷ 4 = 0.25
-
Percentage: 0.25 × 100 = 25%
Therefore, the ratio 15:45 is equivalent to 25%. Notice how the process remains consistent regardless of the numbers involved.
Dealing with Ratios Involving Larger Numbers
When dealing with larger numbers, a calculator becomes extremely helpful. For instance, let's convert the ratio 275:1100 into a percentage:
-
Total: 275 + 1100 = 1375
-
Fraction: 275/1375
-
Simplification (Using a Calculator): A calculator can help simplify this fraction quickly. It simplifies to 11/55, and further to 1/5.
-
Decimal: 1 ÷ 5 = 0.2
-
Percentage: 0.2 × 100 = 20%
So, 275:1100 equals 20%.
Frequently Asked Questions (FAQs)
- Q: What if the ratio involves decimals?
A: The process remains the same. For instance, if you have a ratio of 2.5:10, you would treat it like any other ratio: find the total (12.5), create the fraction (2.5/12.5), simplify, convert to a decimal, and finally to a percentage.
- Q: What if the ratio has more than two numbers?
A: While the above examples focus on two-number ratios, the principles extend to ratios with more than two numbers. You simply add all the numbers to find the total and then express each individual number as a fraction of the total, converting each fraction into a percentage.
- Q: Why is rounding sometimes necessary?
A: Many decimal conversions result in repeating decimals (like in our 6:30 example). Rounding to a reasonable number of decimal places (usually one or two) is necessary for practicality and clarity. The context will often dictate the appropriate level of precision.
Conclusion: Mastering Ratio-to-Percentage Conversions
Converting ratios to percentages is a fundamental mathematical skill with widespread applicability. By understanding the steps involved – finding the total, forming a fraction, simplifying, converting to a decimal, and finally to a percentage – you can confidently tackle this conversion in various contexts. Remember that practice is key to mastering this skill, so try working through different ratios to solidify your understanding. The ability to perform these calculations accurately and efficiently will significantly enhance your problem-solving capabilities in many aspects of life and work.
Latest Posts
Latest Posts
-
49 Degrees Celsius In Fahrenheit
Sep 23, 2025
-
5 9 As A Percent
Sep 23, 2025
-
Do You Capitalize A Season
Sep 23, 2025
-
Alex Rider Books In Order
Sep 23, 2025
-
Presents That Start With M
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6 30 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.