5 9 As A Percent
sportsmenna
Sep 23, 2025 · 5 min read
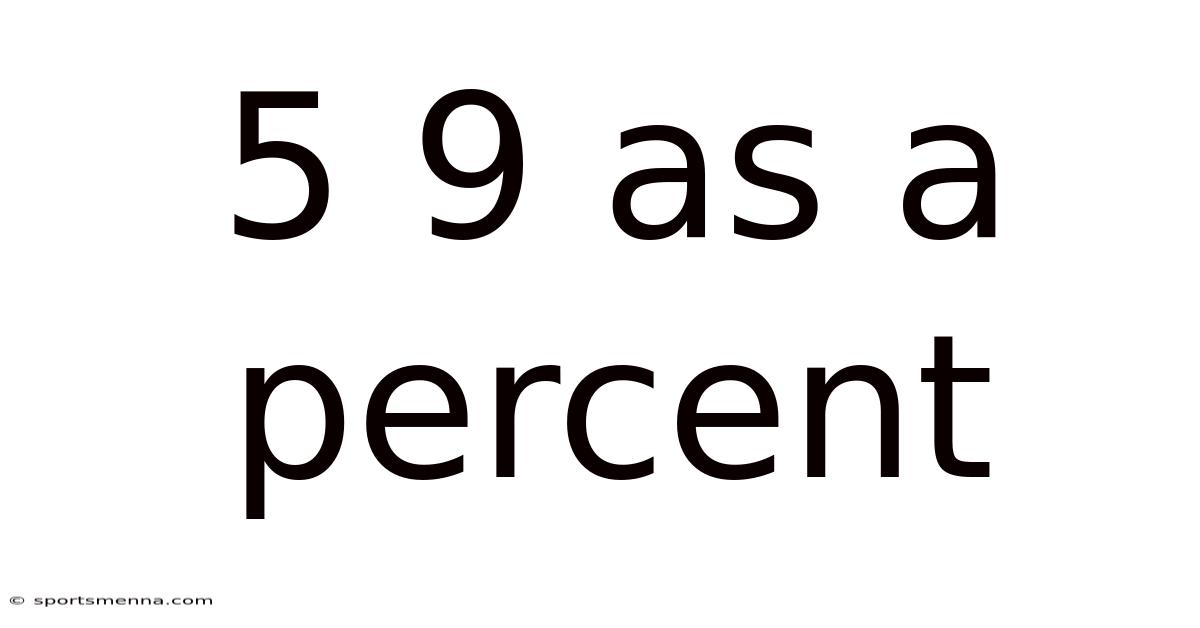
Table of Contents
Understanding 5/9 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across numerous fields, from finance and statistics to everyday calculations. This article will provide a thorough explanation of how to convert the fraction 5/9 into a percentage, exploring different methods and delving into the underlying concepts. We will also cover related concepts and answer frequently asked questions, making this a comprehensive resource for anyone seeking a clear understanding of this mathematical operation. By the end, you'll not only know the answer but also understand the why behind the calculation.
Introduction: Fractions, Decimals, and Percentages – A Trifecta
Before diving into the specifics of converting 5/9, let's briefly review the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Express a part of a whole as a ratio of two numbers (numerator/denominator). For example, 5/9 represents 5 parts out of a total of 9 parts.
-
Decimals: Express a part of a whole using a base-10 system. Decimals use a point (.) to separate whole numbers from fractional parts.
-
Percentages: Express a part of a whole as a portion of 100. The symbol "%" denotes a percentage.
Understanding the interconnectivity of these three forms is crucial for effective mathematical manipulation. They are all interchangeable; one can easily be converted to another.
Method 1: Converting 5/9 to a Decimal, then to a Percentage
This is arguably the most straightforward method. We first convert the fraction 5/9 into a decimal, and then convert the decimal to a percentage.
-
Division: Divide the numerator (5) by the denominator (9). This gives us: 5 ÷ 9 = 0.55555... (This is a repeating decimal).
-
Rounding (optional): Since the decimal is repeating, we can round it to a certain number of decimal places for practicality. Rounding to three decimal places, we get 0.556.
-
Converting to Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol. So, 0.556 x 100 = 55.6%.
Therefore, 5/9 is approximately 55.6%. Remember, this is an approximation due to the rounding of the repeating decimal.
Method 2: Using Proportions to Find the Percentage
This method uses the concept of proportions to directly solve for the percentage. We set up a proportion where the fraction 5/9 is equal to x/100, where 'x' represents the percentage we're trying to find.
-
Setting up the Proportion: We write the proportion as: 5/9 = x/100
-
Cross-Multiplication: We cross-multiply to solve for x: 9x = 500
-
Solving for x: Divide both sides by 9: x = 500/9
-
Calculating and Converting: 500/9 = 55.555... Multiplying by 100 (to express it as a percentage) gives us approximately 55.56%.
Again, we encounter a repeating decimal, leading to a slight approximation depending on the level of rounding. This method confirms the result obtained through the previous method.
Method 3: Understanding the Concept of Percentage Increase/Decrease (Contextual Application)
While the previous methods focus on the direct conversion, understanding the contextual application of percentage is vital. Let's imagine a scenario where 5/9 represents a fraction of a total quantity. For instance, if there are 9 apples, and 5 of them are red, what percentage of apples are red?
This scenario directly applies the fraction 5/9. The process remains the same as the previous methods: 5/9 converted to a percentage will represent the percentage of red apples. The result, approximately 55.6%, means that about 55.6% of the apples are red.
The Significance of Repeating Decimals and Rounding
The fraction 5/9 results in a repeating decimal (0.555...). This is because 9 is not a factor of 10, 100, 1000, and so on. This means the decimal representation will continue indefinitely. Rounding is necessary for practical purposes, but it's essential to remember that the rounded percentage is an approximation, not an exact value. The more decimal places you use, the more accurate your approximation will be.
Applying the Knowledge: Real-World Examples
The conversion of fractions to percentages is essential in many real-world applications:
-
Finance: Calculating interest rates, discounts, and profit margins often involves converting fractions to percentages.
-
Statistics: Expressing data as percentages is crucial for data analysis and interpretation. For example, analyzing survey results, where 5 out of 9 respondents prefer a certain product, translates directly to the percentage calculation.
-
Science: Expressing experimental results or measurements as percentages is standard practice.
-
Everyday Life: Calculating tips, discounts, or sales often requires converting fractions to percentages. For example, if a store offers a 1/3 discount, converting this to a percentage (approximately 33.33%) makes it easier to calculate the final price.
Frequently Asked Questions (FAQ)
- Q: Why is 5/9 a repeating decimal?
A: Because 9 is not a factor of any power of 10 (10, 100, 1000, etc.). When performing the division, the remainder never becomes zero, resulting in a repeating pattern.
- Q: How accurate does my percentage need to be?
A: The required accuracy depends on the context. In some situations, a rough approximation might suffice (e.g., estimating a tip), while in others, higher precision is necessary (e.g., calculating financial returns).
- Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have the functionality to perform this conversion directly. You simply enter the fraction and then convert it to a percentage using the appropriate function.
- Q: What if I have a more complex fraction?
A: The same principles apply. You would first convert the complex fraction into a simpler fraction (if possible) and then follow the steps outlined above to convert it to a decimal and then to a percentage.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions like 5/9 to percentages is a fundamental skill in mathematics with wide-ranging applications. By understanding the different methods – using decimal conversion, proportions, or applying the conceptual understanding to real-world scenarios – you gain a deeper comprehension beyond simply obtaining the answer (approximately 55.6%). Remember to consider the context to determine the appropriate level of rounding for your calculations. This comprehensive guide aims to not just provide the answer but to empower you with the knowledge and confidence to tackle similar fraction-to-percentage conversions in the future. The ability to accurately perform this conversion will serve you well in various academic and professional endeavors.
Latest Posts
Latest Posts
-
Black Versus White Sesame Seeds
Sep 23, 2025
-
Christmas Things Starting With P
Sep 23, 2025
-
Quando What Does It Mean
Sep 23, 2025
-
18 Cm How Many Inches
Sep 23, 2025
-
How Big Is 6 Cm
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 9 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.