6 20 As A Decimal
sportsmenna
Sep 22, 2025 · 5 min read
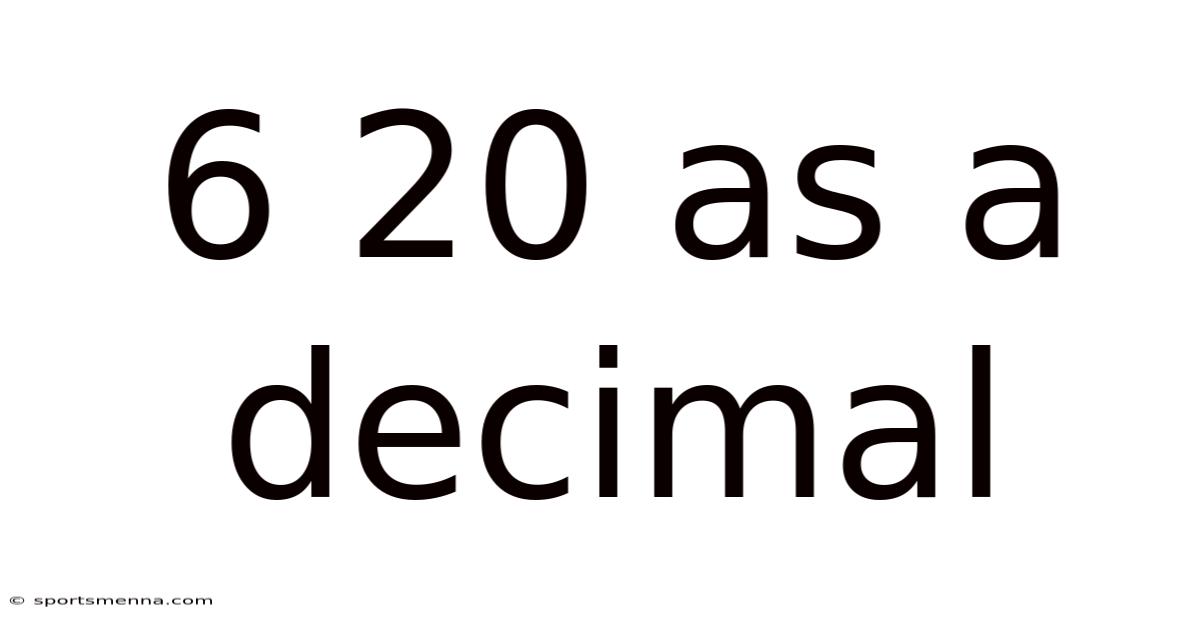
Table of Contents
Understanding 6 20 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning various fields, from everyday calculations to complex scientific computations. This comprehensive guide will delve into the process of converting the mixed number 6 20 (six and twenty) into its decimal equivalent, exploring the underlying concepts and providing practical examples. We’ll also address common misconceptions and answer frequently asked questions to ensure a thorough understanding of this mathematical operation. This guide aims to equip you with the knowledge and confidence to tackle similar conversions with ease.
Understanding Mixed Numbers and Decimals
Before we proceed with the conversion, let's clarify some key terms. A mixed number combines a whole number and a fraction, like 6 20. A decimal, on the other hand, represents a number using base-ten notation, where a decimal point separates the whole number part from the fractional part. For example, 6.5 is a decimal where 6 is the whole number part and .5 represents the fractional part (five-tenths).
The process of converting a mixed number to a decimal involves two key steps: converting the fraction to a decimal and then adding the whole number part.
Step-by-Step Conversion of 6 20 to Decimal
The mixed number 6 20 can be interpreted as 6 + 20. To convert this to a decimal, we focus on the fraction 20. The first step is to convert the fraction into an improper fraction:
-
Convert to an Improper Fraction: An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). To convert 20 into an improper fraction, we recognize that 20 is simply 20/1. Thus, we have 6 + 20/1.
-
Simplify the Fraction (if possible): In this case, the fraction 20/1 is already in its simplest form. However, many fractions can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For instance, if we had 6 ⁴⁄₈, we would simplify the fraction to 6 ½ because the GCD of 4 and 8 is 4.
-
Divide the Numerator by the Denominator: Now, to convert the fraction to a decimal, we simply divide the numerator by the denominator: 20 ÷ 1 = 20.
-
Combine with the Whole Number: Finally, we combine the result from step 3 with the whole number part of our mixed number: 6 + 20 = 26.
Therefore, 6 20 as a decimal is 26.0. The ".0" indicates that there is no fractional part remaining after the conversion.
Alternative Method: Using Decimal Representation Directly
While the previous method is straightforward, another approach involves understanding the fraction directly. The fraction 20/1 represents twenty wholes. Therefore, adding this to the whole number 6 results in 26 directly, without the need for explicit division. This underscores that fractions with a denominator of 1 simply represent whole numbers.
Understanding the Concept of Division in Decimal Conversion
The division step in converting a fraction to a decimal is crucial. It essentially represents how many times the denominator "fits" into the numerator. In the case of 20/1, the denominator (1) fits into the numerator (20) exactly 20 times. However, when dealing with fractions where the denominator does not divide evenly into the numerator, the result will be a decimal with a fractional part. For example:
- 1/2 = 0.5 (the denominator 2 fits into the numerator 1, 0.5 times)
- 1/3 = 0.333... (a repeating decimal)
- 1/4 = 0.25 (the denominator 4 fits into the numerator 1, 0.25 times)
This division process lies at the heart of converting any fraction to its decimal equivalent.
Expanding on Decimal Representation: Significant Figures and Rounding
While 26.0 is the precise decimal representation of 6 20, in many practical applications, we encounter numbers with more complex decimal parts. Understanding significant figures and rounding becomes crucial in these situations.
-
Significant Figures: These are the digits in a number that carry meaning contributing to its precision. For instance, in the measurement 12.345 cm, there are five significant figures.
-
Rounding: When dealing with decimals that extend beyond a required level of precision, rounding helps simplify the number. Common rounding rules involve considering the digit after the desired place value. If that digit is 5 or greater, we round up; otherwise, we round down.
For example, if we needed to round 12.345 to two decimal places, we would obtain 12.35.
Applications of Decimal Conversions
The ability to convert fractions to decimals is fundamental in many fields:
- Finance: Calculating interest rates, discounts, and proportions.
- Engineering: Precision measurements and calculations.
- Science: Representing experimental data and conducting scientific computations.
- Everyday Life: Calculating percentages, splitting bills, and understanding proportions.
Frequently Asked Questions (FAQ)
Q1: What if the fraction part of the mixed number is not a whole number?
A1: Follow the same steps. Convert the fraction to a decimal by dividing the numerator by the denominator. For example, for the mixed number 3 ½, you would divide 1 by 2 (0.5) and then add the whole number 3, resulting in 3.5.
Q2: What are repeating decimals?
A2: Repeating decimals occur when the division of the numerator by the denominator produces a sequence of digits that repeats infinitely. For example, 1/3 = 0.333... (the digit 3 repeats indefinitely). These are often represented with a bar over the repeating digits (e.g., 0.̅3).
Q3: How do I convert a decimal back to a fraction?
A3: To convert a decimal to a fraction, first, write the decimal as a fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.), depending on the number of digits after the decimal point. Then, simplify the fraction to its lowest terms. For example, 0.75 can be written as 75/100, which simplifies to ¾.
Q4: Can I use a calculator for decimal conversions?
A4: Yes, calculators are valuable tools for converting fractions to decimals. Simply divide the numerator by the denominator. However, understanding the underlying mathematical principles remains crucial.
Conclusion
Converting the mixed number 6 20 to a decimal is a straightforward process involving converting the fraction to its decimal equivalent and adding the whole number part. The result, 26.0, highlights the concept of fractions with a denominator of 1 representing whole numbers. Understanding this conversion is vital for various applications in mathematics and beyond. This guide has provided a thorough explanation, addressing common questions and demonstrating the practical applications of this essential mathematical skill. Remember to practice regularly to master this crucial conversion skill and expand your mathematical understanding.
Latest Posts
Latest Posts
-
35 Kg How Many Pounds
Sep 22, 2025
-
What Do 3 Crows Mean
Sep 22, 2025
-
Formula For Respiration In Plants
Sep 22, 2025
-
21 30 As A Percentage
Sep 22, 2025
-
8 Out Of 15 Percentage
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 6 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.