8 Out Of 15 Percentage
sportsmenna
Sep 22, 2025 · 5 min read
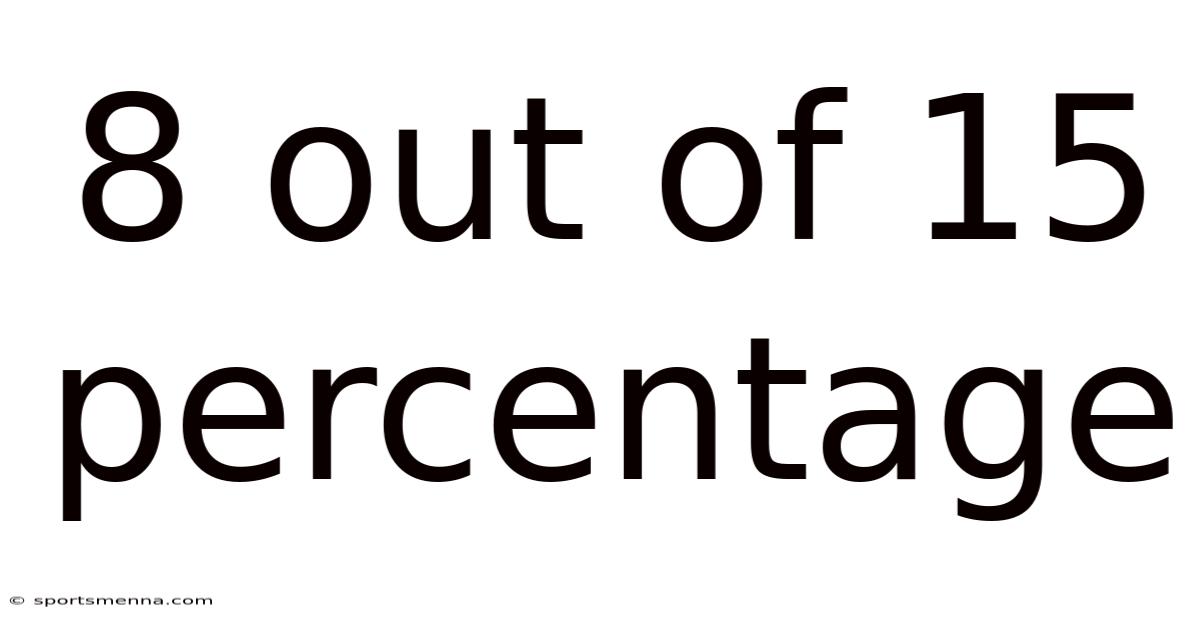
Table of Contents
Understanding 8 out of 15: Fractions, Percentages, and Real-World Applications
What does 8 out of 15 actually mean? This seemingly simple question touches upon fundamental mathematical concepts crucial for everyday life, from understanding sales discounts to interpreting test scores and comprehending statistical data. This article will delve into the intricacies of calculating 8 out of 15 as a fraction, percentage, and decimal, exploring different methods and providing real-world examples to solidify your understanding. We'll also address common misconceptions and offer practical applications to enhance your mathematical proficiency.
Representing 8 out of 15: From Fraction to Percentage
The phrase "8 out of 15" directly translates to a fraction: 8/15. This fraction represents the ratio of a part (8) to a whole (15). Understanding fractions is the cornerstone of understanding percentages and decimals.
Converting the Fraction to a Percentage:
To convert the fraction 8/15 into a percentage, we need to express it as a fraction with a denominator of 100. This involves the following steps:
-
Divide the numerator by the denominator: 8 ÷ 15 ≈ 0.5333
-
Multiply the result by 100: 0.5333 x 100 = 53.33%
Therefore, 8 out of 15 is approximately 53.33%. The "approximately" is crucial because the decimal representation of 8/15 is a repeating decimal (0.5333...). For most practical purposes, rounding to two decimal places (53.33%) is sufficient.
Converting the Fraction to a Decimal:
Converting 8/15 to a decimal simply involves performing the division: 8 ÷ 15 ≈ 0.5333. This decimal representation directly reflects the proportion of 8 out of 15.
Different Methods for Calculating Percentage
While the method described above is the most straightforward, other methods can be used, particularly when dealing with more complex scenarios. Let's explore a few:
Method 1: Direct Proportion
This method is conceptually simple and useful for understanding the underlying relationship. We set up a proportion:
8/15 = x/100
Where 'x' represents the percentage we want to find. Solving for 'x' involves cross-multiplication:
15x = 800
x = 800/15 ≈ 53.33
Method 2: Using a Calculator
Most calculators have a percentage function. Simply input 8 ÷ 15 and then multiply the result by 100 to obtain the percentage.
Method 3: Using a Spreadsheet Program
Spreadsheet programs like Microsoft Excel or Google Sheets offer built-in functions for calculating percentages. The formula =8/15*100 would directly yield the percentage.
Real-World Applications of 8 out of 15 (53.33%)
Understanding how to calculate and interpret 8 out of 15 has widespread practical applications:
-
Test Scores: Imagine a student answered 8 questions correctly out of 15 on a quiz. Their score would be 53.33%. This allows for easy comparison with other students and assessment of performance.
-
Sales and Discounts: A store might offer a 53.33% discount on an item. Understanding this percentage allows consumers to calculate the final price.
-
Statistical Analysis: In surveys or polls, 8 out of 15 respondents might choose a particular option. This data can be expressed as a percentage to understand the proportion of respondents holding that view.
-
Project Completion: If a project has 15 tasks and 8 are completed, 53.33% of the project is finished. This allows for tracking progress and identifying potential delays.
-
Sports Statistics: In sports, 8 out of 15 attempted shots made could represent a player's shooting percentage.
-
Manufacturing and Quality Control: If 8 out of 15 products pass quality checks, the pass rate is 53.33%. This helps identify areas needing improvement in the manufacturing process.
Addressing Common Misconceptions
A common mistake is to simply divide 8 by 15 and interpret the result as a percentage without multiplying by 100. Remember, percentages represent parts per hundred. Always multiply the decimal result by 100 to express it as a percentage.
Another misconception involves confusing the terms "fraction," "decimal," and "percentage." While they represent the same proportion, they use different formats: fractions use a numerator and denominator, decimals use a base-ten system, and percentages express the proportion per hundred.
Further Exploration and Advanced Concepts
While 8/15 is a relatively simple fraction, the principles discussed here apply to more complex fractions and percentages. For example, understanding how to work with fractions with larger numbers, or fractions involving mixed numbers, requires a grasp of the fundamental concepts explained above.
Exploring topics like:
- Compound interest: This involves calculating interest on both the principal and accumulated interest, leading to exponential growth.
- Probability: Understanding the likelihood of events occurring can often be expressed as percentages or fractions.
- Statistical inference: Drawing conclusions about populations based on samples involves working with percentages and proportions.
These are advanced mathematical concepts that build upon the foundational understanding of fractions and percentages.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 8/15?
A: 8/15 is already in its simplest form, as 8 and 15 share no common factors other than 1.
Q: How can I calculate 8 out of 15 without a calculator?
A: You can use long division to divide 8 by 15, then multiply the result by 100. Alternatively, you can use the proportion method explained earlier.
Q: What if I need to find the percentage of a larger number, such as 8 out of 150?
A: The same principles apply. Divide 8 by 150 and multiply the result by 100 to obtain the percentage.
Q: Is there a way to express 8 out of 15 as a ratio?
A: Yes, the ratio is 8:15. This simply represents the relationship between the two numbers.
Q: Can I use a different denominator besides 100 to convert a fraction to a percentage?
A: While 100 is the standard denominator for percentages (meaning "per hundred"), you could use other denominators, but you'd need to adjust your calculations accordingly. The key is to find a way to express the fraction in terms of a part of a whole.
Conclusion
Understanding how to calculate and interpret 8 out of 15, as a fraction, decimal, and percentage, is a fundamental skill with broad applications across various fields. Mastering this concept provides a solid foundation for tackling more complex mathematical problems and enhances your ability to interpret data and solve real-world problems. The methods and examples discussed in this article aim to equip you with the knowledge and confidence to approach such calculations efficiently and accurately. Remember, practice is key to solidifying your understanding, so try applying these methods to different scenarios and challenge yourself to refine your mathematical skills.
Latest Posts
Latest Posts
-
1 Stone Weight Loss Equivalent
Sep 22, 2025
-
How To Calculate Cross Section
Sep 22, 2025
-
States That Begin With H
Sep 22, 2025
-
Distance From London To Southampton
Sep 22, 2025
-
What Does Brown Color Represent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 15 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.