What Is 75 Of 80
sportsmenna
Sep 22, 2025 · 5 min read
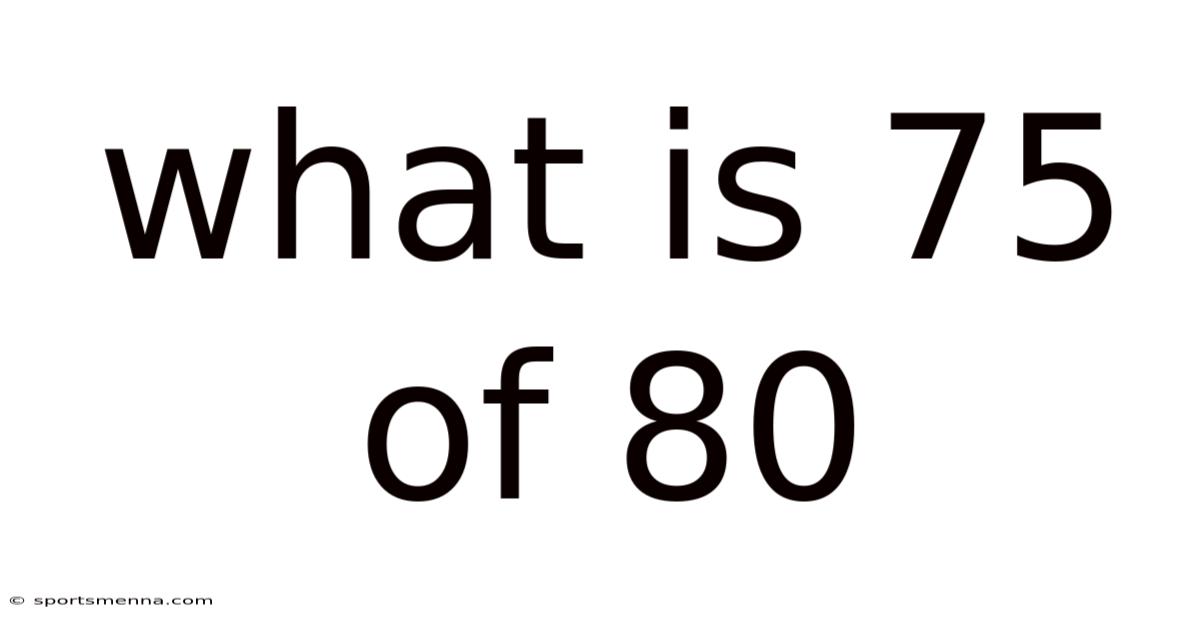
Table of Contents
What is 75% of 80? A Comprehensive Guide to Percentages and Calculations
Finding 75% of 80 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This guide will not only show you how to calculate 75% of 80 using several methods but will also delve into the underlying principles of percentages, offering a deeper understanding of this essential mathematical tool. We'll explore different approaches, discuss real-world applications, and answer frequently asked questions to solidify your understanding. By the end, you'll be confident in calculating percentages and applying this knowledge to various situations.
Understanding Percentages: The Basics
Before we tackle the specific calculation of 75% of 80, let's establish a firm understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding this fundamental relationship between percentages, fractions, and decimals is crucial for performing percentage calculations. Converting between these forms is a key skill that will simplify many problems.
Method 1: Converting to a Decimal
This is arguably the most straightforward method. To find 75% of 80, we first convert the percentage to its decimal equivalent. We do this by dividing the percentage by 100:
75% ÷ 100 = 0.75
Now, we simply multiply this decimal by the number we want to find the percentage of:
0.75 * 80 = 60
Therefore, 75% of 80 is 60.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 75% can be written as 75/100. This fraction can be simplified:
75/100 = 3/4
Now, we multiply this simplified fraction by 80:
(3/4) * 80 = (3 * 80) / 4 = 240 / 4 = 60
Again, we arrive at the answer: 75% of 80 is 60.
Method 3: Finding 10%, then scaling up
This method is particularly useful for mental calculations or when dealing with percentages that are multiples of 10. First, we find 10% of 80:
10% of 80 = (10/100) * 80 = 8
Since 75% is 7.5 times 10%, we multiply our result by 7.5:
8 * 7.5 = 60
This method demonstrates that understanding the relationship between percentages allows for flexible calculation strategies.
Method 4: Using Proportions
Proportions offer a powerful, albeit slightly more advanced, approach. We set up a proportion where 'x' represents the unknown value (75% of 80):
75/100 = x/80
To solve for x, we cross-multiply:
75 * 80 = 100 * x
6000 = 100x
x = 6000 / 100
x = 60
Thus, using proportions, we again confirm that 75% of 80 is 60.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Retailers frequently advertise discounts as percentages. For instance, a "25% off" sale means you pay 75% of the original price. Calculating the final price requires understanding percentage calculations.
-
Taxes and Interest: Taxes on purchases, income tax, and interest on loans or savings accounts are all expressed as percentages. Accurately calculating these amounts requires proficiency in percentage calculations.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. Understanding percentages helps in comprehending data represented as proportions or rates.
-
Financial Planning: Budgeting, investment returns, and loan repayments all involve working with percentages. Strong percentage skills are crucial for effective financial planning.
-
Science and Engineering: Many scientific and engineering applications utilize percentages to express concentrations, efficiencies, or changes in quantities.
Further Exploration: Beyond 75% of 80
While we've focused on calculating 75% of 80, the principles discussed are broadly applicable. Let's explore some related scenarios:
-
Calculating other percentages of 80: Using the methods outlined above, you can easily calculate any percentage of 80. Simply replace 75% with the desired percentage and follow the same steps.
-
Calculating 75% of different numbers: The methods discussed can be applied to find 75% of any number. Replace 80 with the new number and proceed with the chosen method.
-
Finding the original amount given a percentage: Let's say you know that 75% of a number is 60. You can use proportions or algebraic equations to determine the original number.
Frequently Asked Questions (FAQ)
Q1: What is the easiest method to calculate percentages?
A1: The easiest method often depends on the specific numbers and your personal preference. Converting to a decimal (Method 1) is generally straightforward for most calculations. However, using fractions (Method 2) can be simpler for certain percentages like 25%, 50%, and 75%.
Q2: Are there any online calculators for percentages?
A2: Yes, numerous online percentage calculators are readily available. These calculators can quickly compute percentages and are useful for verifying your calculations or for solving more complex problems.
Q3: How can I improve my skills in calculating percentages?
A3: Consistent practice is key. Start with simple examples and gradually increase the complexity of the calculations. Understanding the different methods will allow you to choose the most efficient approach for each problem. You can also utilize online resources, such as practice worksheets and tutorials.
Q4: What if the percentage is not a whole number, like 75.5%?
A4: The methods remain the same; you would simply convert 75.5% to its decimal equivalent (0.755) and multiply it by the number.
Q5: How are percentages used in everyday life beyond shopping?
A5: Percentages are used extensively in finance (interest rates, loan calculations), health (body fat percentage, medication dosages), and even cooking (adjusting recipes). Essentially, any situation requiring proportional representation or comparison of quantities will likely involve percentages.
Conclusion
Finding 75% of 80, while seemingly a simple task, serves as a gateway to understanding the broader world of percentage calculations. Mastering this concept is essential for success in various academic and professional fields. By understanding the different methods—converting to decimals, using fractions, employing proportions, or even scaling from 10%—you equip yourself with versatile tools to solve a wide range of percentage-related problems. Remember, consistent practice and a solid grasp of the underlying principles are the keys to building confidence and proficiency in this crucial mathematical area. Don't hesitate to explore different methods and find the ones that work best for your learning style and the specific problem you are solving. The more you practice, the easier and more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
150 000 Miles In Km
Sep 22, 2025
-
Long Layered Hair Side Bangs
Sep 22, 2025
-
Mix Of Black And White
Sep 22, 2025
-
Dimensions Of A 2p Coin
Sep 22, 2025
-
Is Quin A Scrabble Word
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.