What Is 70 Of 50
sportsmenna
Sep 20, 2025 · 6 min read
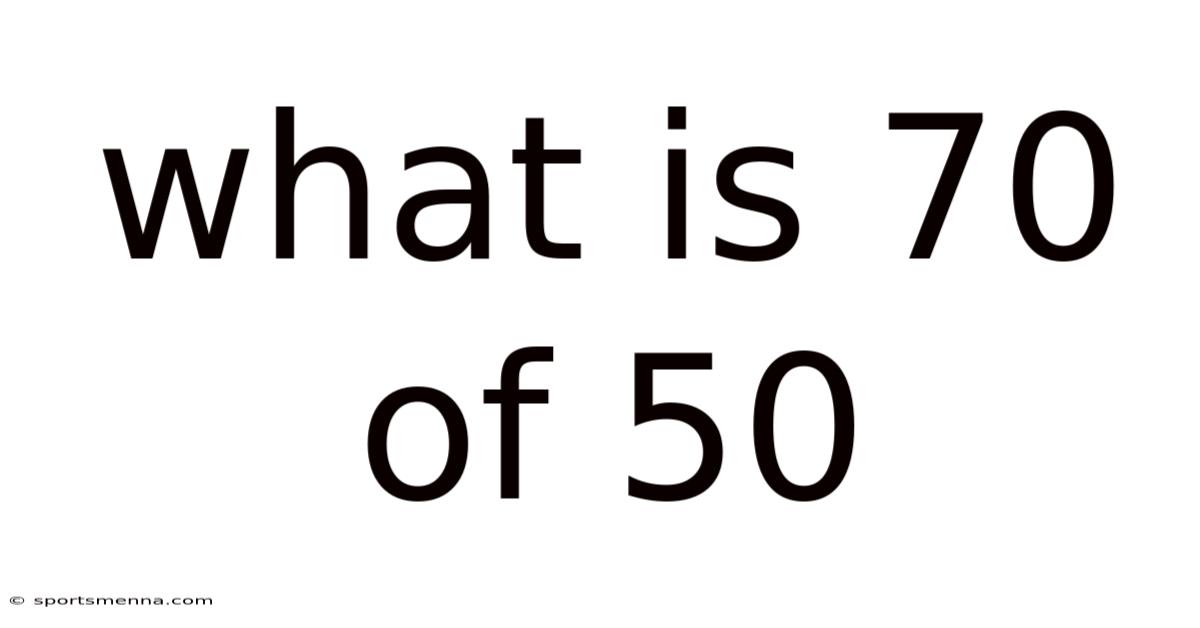
Table of Contents
What is 70% of 50? A Deep Dive into Percentages and Their Applications
Finding 70% of 50 might seem like a simple calculation, but understanding the underlying principles of percentages opens the door to a wide range of applications in mathematics, science, finance, and everyday life. This article will not only answer the question directly but will also delve into the various methods of calculating percentages, explaining the concepts in a clear and accessible way, suitable for learners of all levels. We'll explore different approaches, providing a comprehensive understanding of percentages and their practical use.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ( per centum in Latin). So, 70% means 70 out of 100, or 70/100. This fraction can be simplified to 7/10. Understanding this fundamental concept is crucial for tackling percentage problems.
Method 1: Using Fractions
The most straightforward method to calculate 70% of 50 is to convert the percentage into a fraction and then multiply it by the number.
-
Step 1: Convert the percentage to a fraction: 70% is equal to 70/100.
-
Step 2: Simplify the fraction (optional but helpful): 70/100 simplifies to 7/10.
-
Step 3: Multiply the fraction by the number: (7/10) * 50 = 350/10 = 35
Therefore, 70% of 50 is 35.
Method 2: Using Decimals
Another common approach involves converting the percentage to a decimal and then multiplying.
-
Step 1: Convert the percentage to a decimal: To convert a percentage to a decimal, divide the percentage by 100. 70% divided by 100 is 0.7.
-
Step 2: Multiply the decimal by the number: 0.7 * 50 = 35
Again, we arrive at the answer: 70% of 50 is 35.
Method 3: Using Proportions
This method is particularly helpful for understanding the underlying relationship between percentages and their corresponding values. We can set up a proportion:
-
Step 1: Set up the proportion: We can represent the problem as a proportion: x/50 = 70/100, where 'x' represents the unknown value (70% of 50).
-
Step 2: Cross-multiply: Multiply the numerator of one fraction by the denominator of the other, and vice-versa: 100x = 70 * 50
-
Step 3: Solve for x: 100x = 3500. Divide both sides by 100 to isolate x: x = 35
This confirms that 70% of 50 is 35.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-life scenarios. Let's explore some examples:
-
Sales and Discounts: Imagine a store offering a 70% discount on an item originally priced at $50. Using our calculation, the discount amount would be $35, making the final price $15 ($50 - $35). Understanding percentage discounts helps consumers make informed purchasing decisions.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount involves finding a percentage of the total amount.
-
Financial Investments: Interest rates on savings accounts, loans, and investments are expressed as percentages. Calculating interest earned or paid requires understanding percentage calculations. For example, calculating the interest earned on a $50 investment with a 7% annual interest rate would involve finding 7% of $50.
-
Statistics and Data Analysis: Percentages are extensively used to represent data in graphs, charts, and reports. Understanding percentage changes helps in analyzing trends and making informed decisions based on data. For instance, understanding the percentage increase or decrease in sales, population growth or market share is critical for many businesses and researchers.
-
Scientific Calculations: Percentages are used in many scientific contexts, including expressing concentrations of solutions, analyzing experimental data, and calculating error margins.
-
Everyday Life: Percentages appear frequently in our daily lives – from calculating tips in restaurants to understanding nutritional information on food labels. Knowing how to calculate percentages helps us to make better decisions and to better understand the world around us.
Advanced Percentage Calculations: Beyond the Basics
While finding 70% of 50 is a relatively straightforward calculation, more complex scenarios might involve finding a percentage of a percentage or working backwards to find the original value based on a percentage.
Finding a percentage of a percentage: This involves performing multiple percentage calculations sequentially. For instance, finding 20% of 70% of 50 would require calculating 70% of 50 first (which is 35), and then calculating 20% of 35.
Finding the original value: If you know a percentage of a value and the resulting amount, you can use algebra to find the original value. For example, if 70% of a number is 35, you can set up the equation: 0.7x = 35, and solve for x. This technique is frequently useful when analyzing sales, discounts, or tax scenarios.
Common Mistakes to Avoid When Calculating Percentages
-
Confusing Percentage and Decimal: Ensure you correctly convert between percentages and decimals. Remember to divide by 100 when converting percentages to decimals and multiply by 100 when converting decimals to percentages.
-
Incorrect Order of Operations: If your calculation involves multiple steps, follow the order of operations (PEMDAS/BODMAS) to ensure accuracy.
-
Rounding Errors: While rounding can simplify calculations, be aware that rounding errors can accumulate and lead to inaccuracies, especially when dealing with multiple calculations. Try to retain as many decimal places as possible during intermediate steps before rounding to the final answer.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
A1: To calculate a percentage increase, find the difference between the new value and the original value, divide the difference by the original value, and then multiply by 100. For a percentage decrease, follow the same process, but the result will be negative.
Q2: Can I use a calculator to find percentages?
A2: Yes, most calculators have a percentage function (%) that simplifies percentage calculations. However, understanding the underlying principles is still crucial for interpreting the results and applying the concepts in various contexts.
Q3: What if the percentage is greater than 100%?
A3: A percentage greater than 100% indicates that the value is more than the original value. For example, 150% of 50 would be 1.5 * 50 = 75.
Q4: Are there any online resources or tools to help me with percentage calculations?
A4: While external resources are not allowed within this article, many websites and apps provide percentage calculators and tutorials that can aid in understanding and practicing percentage calculations.
Conclusion
This in-depth exploration of percentage calculations demonstrates that finding 70% of 50, while seemingly simple, reveals fundamental mathematical concepts with broad applicability. Mastering percentage calculations enhances your skills in various fields, enabling you to analyze data, make informed financial decisions, and interpret information presented in percentages. Remember the various methods – using fractions, decimals, or proportions – and practice to develop fluency and confidence in handling percentage problems. Understanding percentages is not just about numbers; it's about understanding proportions, relationships, and how these concepts impact our daily lives.
Latest Posts
Latest Posts
-
Does Hot Chocolate Has Caffeine
Sep 20, 2025
-
Closest International Airport To Eindhoven
Sep 20, 2025
-
Happy Birthday In Arabic Language
Sep 20, 2025
-
Back Of The House Definition
Sep 20, 2025
-
Convert Metre To Square Metres
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.