What Is 30 Of 25
sportsmenna
Sep 21, 2025 · 5 min read
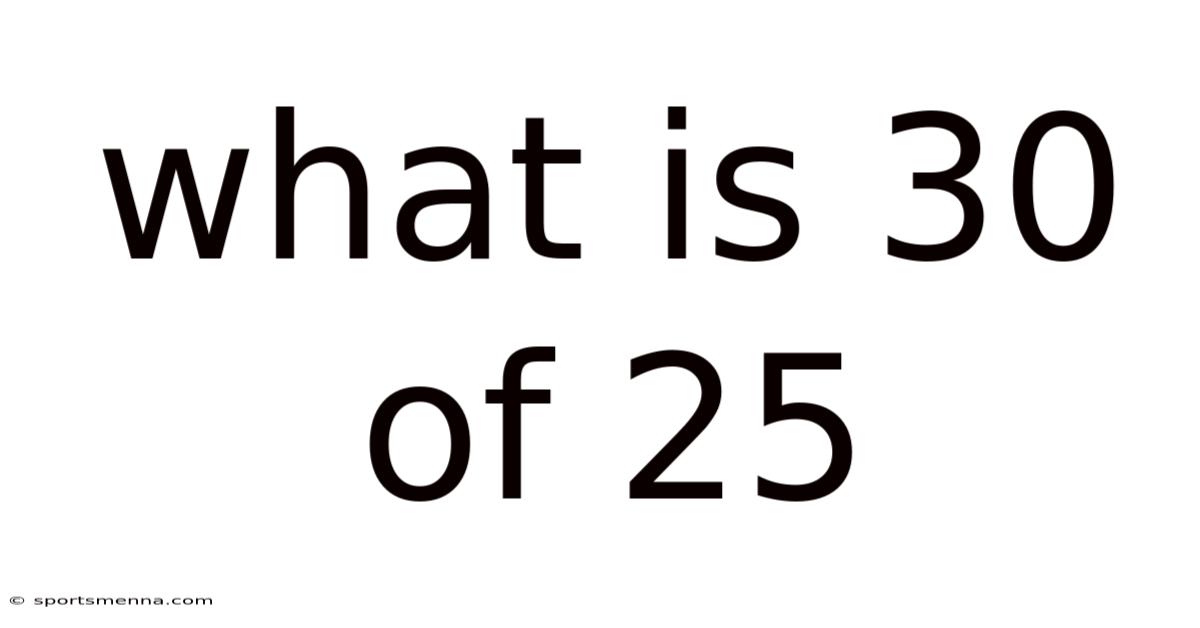
Table of Contents
What is 30% of 25? A Deep Dive into Percentages and Their Applications
Finding 30% of 25 might seem like a simple calculation, but understanding the underlying concepts of percentages is crucial for various aspects of life, from budgeting and finance to understanding data and statistics. This article will not only solve this specific problem but also delve into the broader world of percentages, exploring different calculation methods, real-world applications, and addressing frequently asked questions. This comprehensive guide will empower you to confidently tackle similar percentage problems in the future.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred". So, 30% means 30 out of 100, which can be written as the fraction 30/100 or the decimal 0.30. Understanding this fundamental concept is key to solving any percentage problem.
Method 1: Using Decimal Conversion
This is perhaps the most straightforward method. We convert the percentage to a decimal and then multiply it by the number we're interested in finding the percentage of.
Steps:
-
Convert the percentage to a decimal: To convert 30% to a decimal, we divide 30 by 100: 30 ÷ 100 = 0.30
-
Multiply the decimal by the number: Now, multiply the decimal (0.30) by 25: 0.30 x 25 = 7.5
Therefore, 30% of 25 is $\boxed{7.5}$.
Method 2: Using Fraction Conversion
This method involves converting the percentage to a fraction and then performing the multiplication.
Steps:
-
Convert the percentage to a fraction: 30% can be written as the fraction 30/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10: 30/100 = 3/10
-
Multiply the fraction by the number: Now, multiply the simplified fraction (3/10) by 25: (3/10) x 25 = (3 x 25) / 10 = 75/10
-
Simplify the result: The fraction 75/10 can be simplified by dividing both the numerator and denominator by 5: 75/10 = 15/2 = 7.5
Therefore, 30% of 25 is again $\boxed{7.5}$.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the unknown value.
Steps:
-
Set up a proportion: We can set up a proportion as follows:
30/100 = x/25
Where 'x' represents the unknown value (30% of 25).
-
Cross-multiply: Cross-multiply the terms:
30 x 25 = 100x
750 = 100x
-
Solve for x: Divide both sides by 100:
x = 750/100 = 7.5
Therefore, 30% of 25 is once more $\boxed{7.5}$.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in many real-life situations. Here are a few examples:
-
Finance: Calculating interest on loans, savings accounts, or investments. Understanding discounts and sales tax are also heavily reliant on percentages. For instance, if a store offers a 30% discount on a $25 item, you would save $7.50.
-
Data Analysis: Percentages are frequently used to represent data in charts, graphs, and reports. They help to visualize proportions and trends effectively. For example, understanding the percentage of students who passed an exam or the market share of a particular company often involves percentage calculations.
-
Science: Percentages are used in scientific experiments and calculations to express concentrations, efficiencies, or error margins.
-
Everyday Life: Calculating tips at restaurants, figuring out sale prices, or determining the percentage of a task that is complete, all utilize the fundamentals of percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While finding 30% of 25 is a relatively simple calculation, understanding percentages extends to more complex scenarios. For example:
-
Finding the percentage increase or decrease: This involves calculating the difference between two values and expressing it as a percentage of the original value. For example, if the price of an item increased from $25 to $30, the percentage increase is ((30-25)/25) * 100% = 20%.
-
Calculating a value given a percentage and a result: Suppose you know that 30% of a certain number is 7.5. To find that number, you can set up an equation: 0.30 * x = 7.5. Solving for x, you get x = 7.5 / 0.30 = 25.
-
Compound percentages: These involve calculating percentages of percentages, often encountered in compound interest calculations.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a different percentage of 25?
A1: You can use any of the methods described above, simply substituting the desired percentage for 30%. For example, to find 15% of 25, you would calculate 0.15 * 25 = 3.75.
Q2: Are there any online calculators or tools that can help with percentage calculations?
A2: Yes, many free online calculators are available specifically designed for percentage calculations. These can be particularly helpful for more complex calculations.
Q3: Why is understanding percentages important?
A3: Percentages are a fundamental part of numeracy and are used extensively in various fields. Understanding percentages empowers you to make informed decisions in financial matters, interpret data correctly, and solve problems effectively in many aspects of daily life.
Q4: Can I use a calculator to solve these problems?
A4: Absolutely! While the manual calculations demonstrate the underlying concepts, a calculator can significantly speed up the process, especially for more complex percentage problems.
Conclusion
Finding 30% of 25, which equals 7.5, is a straightforward calculation that illustrates the broader concept of percentages. Mastering percentage calculations is a valuable skill with far-reaching applications in finance, data analysis, science, and everyday life. By understanding the different methods for calculating percentages and their real-world implications, you equip yourself with a powerful tool for problem-solving and decision-making. Remember to practice regularly and don't hesitate to utilize available tools and resources to enhance your understanding and efficiency. The more comfortable you become with percentages, the better equipped you'll be to navigate the numerical challenges of the world around you.
Latest Posts
Latest Posts
-
Boots Ponds Cold Cream Cleanser
Sep 21, 2025
-
Nearest Airport To Ipswich England
Sep 21, 2025
-
70 Degrees F In C
Sep 21, 2025
-
Lcm For 7 And 9
Sep 21, 2025
-
Grass Plain In South America
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.