What Is 30 Of 1000
sportsmenna
Sep 20, 2025 · 5 min read
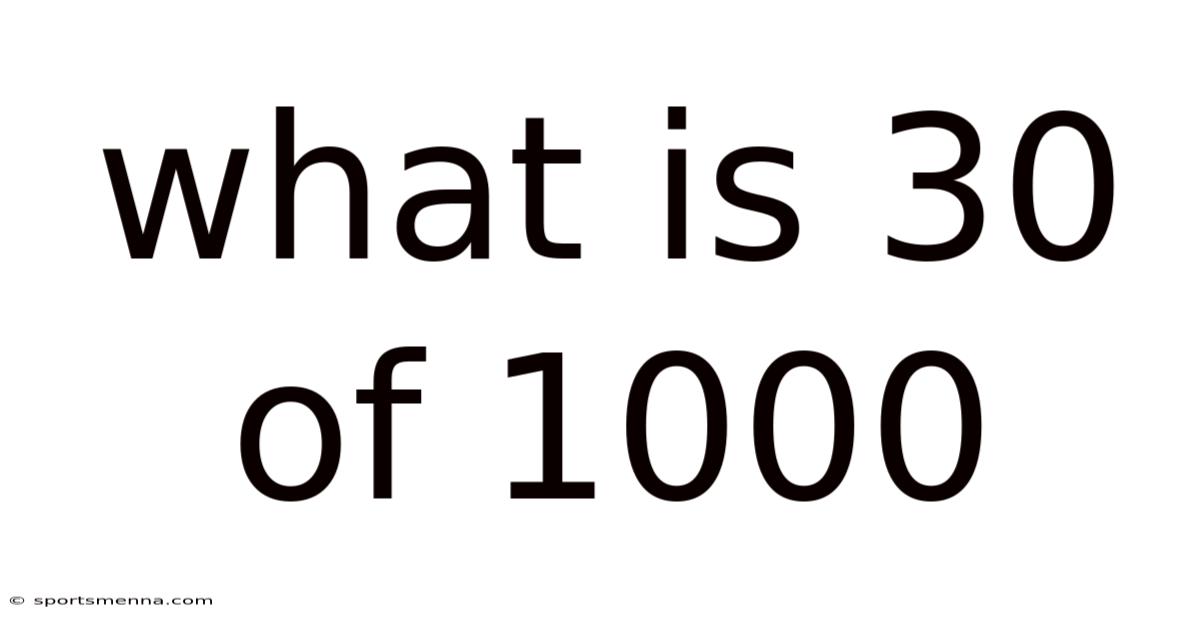
Table of Contents
What is 30 of 1000? Understanding Percentages, Fractions, and Ratios
Finding out "what is 30 of 1000?" might seem like a simple question, but it opens a door to a fundamental understanding of mathematical concepts like percentages, fractions, and ratios. This seemingly basic calculation is actually a gateway to solving more complex problems in various fields, from everyday budgeting to advanced statistical analysis. This article will delve into the different ways to interpret and solve this problem, enriching your understanding of these core mathematical principles.
Understanding the Question: Different Interpretations
The phrase "30 of 1000" can be interpreted in several ways, all leading to different mathematical operations and results. Let's clarify these interpretations before proceeding to the solutions:
-
30 as a part of 1000: This is the most straightforward interpretation. We want to determine what proportion of 1000 is represented by 30. This involves calculating the percentage, fraction, and decimal representation of 30 relative to 1000.
-
30 out of 1000: This phrasing is synonymous with the first interpretation, emphasizing the idea of 30 being a subset of a larger group of 1000.
-
The relationship between 30 and 1000: This interpretation focuses on the ratio between 30 and 1000. This can be expressed as a simplified fraction, a decimal, or a percentage.
Method 1: Calculating the Percentage
The most common way to interpret "30 of 1000" is as a percentage. A percentage represents a fraction of 100. To find the percentage, we follow these steps:
-
Set up a fraction: Express 30 as the numerator (the part) and 1000 as the denominator (the whole): 30/1000
-
Convert the fraction to a decimal: Divide the numerator by the denominator: 30 ÷ 1000 = 0.03
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.03 x 100 = 3%
Therefore, 30 is 3% of 1000. This means that 30 represents 3 out of every 100 items in a group of 1000.
Method 2: Expressing it as a Fraction
Expressing "30 of 1000" as a fraction is a simple yet powerful way to show the relationship between the two numbers. The fraction is already established in the percentage calculation: 30/1000.
However, this fraction can be simplified by finding the greatest common divisor (GCD) of 30 and 1000, which is 10. Dividing both the numerator and the denominator by 10, we get the simplified fraction: 3/100.
This simplified fraction, 3/100, clearly shows that 30 represents three hundredths of 1000. This representation is useful for understanding the proportional relationship between the numbers.
Method 3: Representing it as a Ratio
A ratio expresses the quantitative relationship between two or more values. In this case, the ratio of 30 to 1000 can be written as 30:1000. Like the fraction, this ratio can be simplified by dividing both sides by their GCD (10): 3:100.
This simplified ratio, 3:100, means that for every 3 units of one quantity, there are 100 units of another. This representation is particularly useful when comparing different quantities or proportions.
Method 4: Using Proportions
Proportions offer another way to solve this problem. A proportion is a statement that two ratios are equal. We can set up a proportion to find the equivalent percentage:
30/1000 = x/100
To solve for x (the percentage), cross-multiply:
30 * 100 = 1000 * x
3000 = 1000x
x = 3000/1000 = 3
Therefore, x = 3%, confirming our earlier calculations.
Real-World Applications
Understanding how to calculate "30 of 1000" extends far beyond simple arithmetic exercises. Here are some real-world applications:
-
Business and Finance: Calculating percentages is crucial for analyzing financial statements, determining profit margins, understanding market share, and assessing investment returns. For example, if a company sold 30 out of 1000 products, it can easily calculate the percentage of sales and make adjustments to the marketing strategy.
-
Science and Statistics: Percentages and ratios are fundamental in scientific research for representing data, analyzing experimental results, and interpreting statistical significance. For instance, in a clinical trial, if 30 out of 1000 participants experienced side effects, this can be represented as a percentage to determine the efficacy and safety of a drug.
-
Everyday Life: We encounter percentages and ratios daily. Calculating discounts, understanding sales tax, or determining the proportion of ingredients in a recipe all involve these concepts. For example, knowing 3% of your monthly income is saved could help determine how much money will be saved in a year.
-
Education: Understanding these concepts is fundamental for progressing in mathematics and other quantitative subjects. Mastering these fundamental concepts is crucial for success in secondary education and beyond.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to find the percentage?
A1: Absolutely! Most calculators can perform the division and multiplication required to convert a fraction to a percentage. Simply divide 30 by 1000 and then multiply the result by 100.
Q2: What if the numbers are larger or more complex?
A2: The principles remain the same. Regardless of the size of the numbers, you always divide the part by the whole and then multiply by 100 to find the percentage. For larger numbers, using a calculator is recommended.
Q3: Why is it important to learn these methods?
A3: Understanding percentages, fractions, and ratios is crucial for various aspects of life. These are fundamental mathematical concepts with widespread applications in various academic and professional fields. Mastering these will equip you with essential tools for problem-solving and decision-making.
Q4: Are there other ways to represent the relationship between 30 and 1000?
A4: Yes, you could also use a bar graph or pie chart to visually represent the relationship between 30 and 1000. These visual aids can effectively demonstrate the proportion of 30 relative to 1000.
Conclusion
Determining "what is 30 of 1000?" may seem simple at first glance. However, exploring the different interpretations and solution methods reveals a deeper understanding of percentages, fractions, ratios, and proportions. These core mathematical concepts underpin numerous applications in daily life, various academic disciplines, and professional fields. Mastering these concepts equips you with valuable tools for critical thinking, problem-solving, and effective communication of quantitative information. By understanding the different ways to interpret and solve this problem, you enhance your mathematical literacy and build a strong foundation for tackling more complex challenges. Remember, the key is not just to find the answer (3%), but to grasp the underlying principles and their far-reaching significance.
Latest Posts
Latest Posts
-
How Long Is 45 Cm
Sep 20, 2025
-
1992 How Old Am I
Sep 20, 2025
-
When To Use Sincerely Faithfully
Sep 20, 2025
-
Does Hot Chocolate Has Caffeine
Sep 20, 2025
-
Closest International Airport To Eindhoven
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.