What Is 20 Of 12
sportsmenna
Sep 23, 2025 · 5 min read
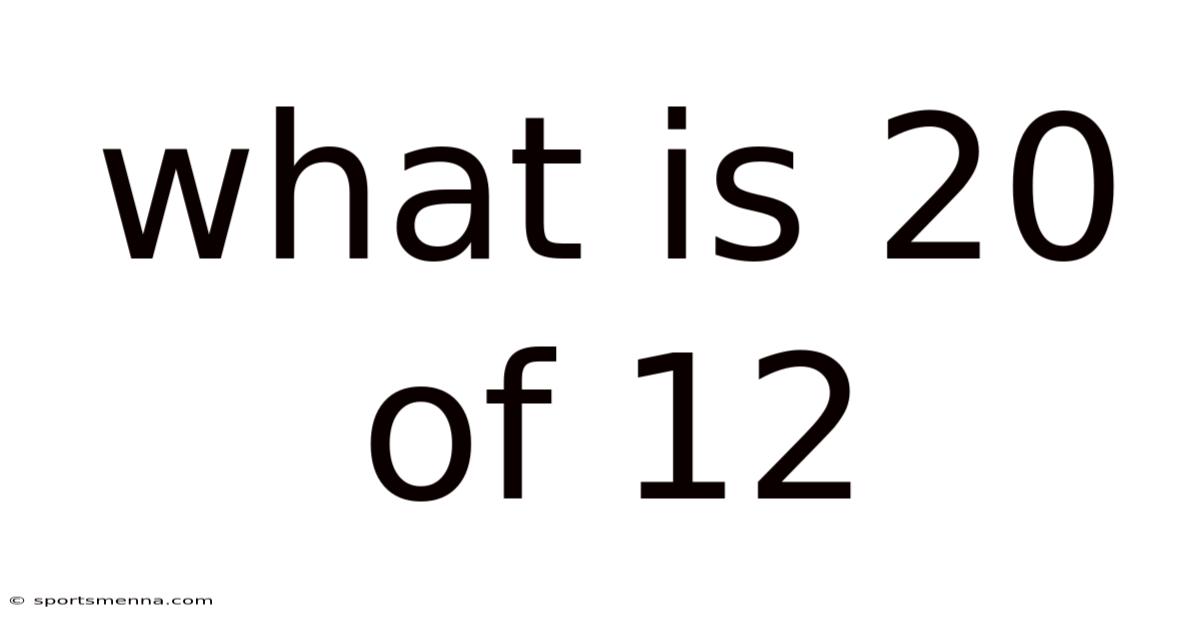
Table of Contents
What is 20 of 12? Unpacking Fractions, Percentages, and Ratios
The seemingly simple question, "What is 20 of 12?" actually opens the door to a deeper understanding of fundamental mathematical concepts: fractions, percentages, and ratios. This seemingly straightforward query allows us to explore these concepts in detail, moving beyond simple calculations to grasp the underlying principles and their practical applications.
This article will not only answer the initial question but also delve into the various interpretations and methods for solving similar problems, focusing on clarity and providing a solid foundation for anyone seeking to improve their mathematical understanding. We'll explore the different ways to approach this problem, highlighting the importance of context and the nuances involved in interpreting mathematical expressions.
Understanding the Ambiguity: Different Interpretations of "Of"
The word "of" in mathematics, particularly when dealing with fractions and percentages, often signifies multiplication. However, the phrasing "20 of 12" lacks precise mathematical notation, leading to several possible interpretations. This ambiguity is crucial to address. We need to consider different scenarios:
-
20 as a fraction of 12: This interpretation implies finding 20/12 of 12. This simplifies to just 20.
-
20% of 12: This is a percentage calculation. Here, "of" signifies multiplication, and we calculate 20% * 12.
-
A ratio of 20 to 12: This interpretation represents a relationship between two numbers. We would express this as 20:12, which can be simplified.
Let's examine each interpretation in detail.
Interpretation 1: 20/12 of 12
This interpretation is perhaps the most straightforward, though potentially unusual. It implies calculating (20/12) * 12.
-
Calculation: The 12s cancel each other out, leaving us with simply 20.
-
Explanation: This method treats "20 of 12" as if it were written as "20/12 * 12." This is a valid mathematical operation, but it's not the typical way this kind of phrase would be understood in common usage.
-
Practical Application: While this interpretation provides a mathematically correct answer, its real-world applicability is limited. It’s more likely a result of a poorly phrased mathematical problem than a standard application.
Interpretation 2: 20% of 12 (Percentage Calculation)
This is the most likely intended meaning of the phrase "20 of 12" within a practical context. It calls for a percentage calculation.
-
Converting Percentage to Decimal: To calculate 20% of 12, we first convert 20% into its decimal equivalent: 20% = 20/100 = 0.20.
-
Multiplication: Next, we multiply the decimal equivalent by 12: 0.20 * 12 = 2.4
-
Explanation: This method uses the standard mathematical interpretation of "of" as multiplication when working with percentages. This is a common and widely used approach.
-
Practical Application: This interpretation has wide-ranging applications. It’s used extensively in financial calculations (discounts, interest, tax), statistics (calculating percentages of populations), and various other fields. For instance, finding a 20% discount on a $12 item would use this calculation.
Interpretation 3: Ratio of 20 to 12 (Ratio and Proportion)
This interpretation focuses on the relationship between 20 and 12, not necessarily a calculation resulting in a single numerical answer.
-
Expressing the Ratio: The ratio of 20 to 12 is written as 20:12 or 20/12.
-
Simplifying the Ratio: To simplify the ratio, we find the greatest common divisor (GCD) of 20 and 12, which is 4. Dividing both numbers by 4 gives us a simplified ratio of 5:3.
-
Explanation: Ratios express the relative size of two or more values. In this context, it shows the proportional relationship between 20 and 12. The simplified ratio 5:3 indicates that for every 5 units of one quantity, there are 3 units of the other.
-
Practical Application: Ratios are used extensively in various fields. They are crucial in scaling recipes, mixing ingredients (e.g., concrete, paint), understanding proportions in maps, and comparing different quantities.
Further Exploration: Extending the Concept
Understanding "20 of 12" allows us to explore related concepts:
-
Proportions: A proportion is a statement of equality between two ratios. We can use the simplified ratio 5:3 to set up proportions and solve for unknown values. For instance, if we have 15 units of one quantity, how many units of the other would we have? We can set up the proportion: 5/3 = x/15. Solving for x gives us x = 25.
-
Fractions and Decimals: This problem highlights the interplay between fractions and decimals. Understanding how to convert between these forms is crucial for various calculations. The conversion of 20% to 0.20 demonstrates this interrelationship.
-
Real-World Applications: The ability to solve percentage problems and understand ratios has profound implications for everyday life. From calculating discounts and taxes to understanding statistical data and interpreting scales on maps, these skills are invaluable.
Frequently Asked Questions (FAQ)
-
Q: What is the most common interpretation of "20 of 12"?
- A: The most common and practical interpretation is 20% of 12, resulting in 2.4.
-
Q: Why is the phrasing "20 of 12" ambiguous?
- A: The word "of" in this context lacks the precision of standard mathematical notation. It doesn't explicitly state whether it's a fraction, percentage, or ratio.
-
Q: How can I avoid ambiguity in similar problems?
- A: Always use clear mathematical notation. Instead of "20 of 12," write "20% of 12" or "20/12 * 12" to ensure clarity.
-
Q: What is the difference between a ratio and a proportion?
- A: A ratio compares two quantities; a proportion is a statement of equality between two ratios.
-
Q: Are there other ways to interpret "20 of 12"?
- A: While less likely, one could interpret it as the number 20 being somehow connected or related to the number 12, with no direct mathematical operation implied. This is highly context-dependent.
Conclusion: Mastering the Fundamentals
The seemingly simple question "What is 20 of 12?" has led us on a journey through several important mathematical concepts. While the lack of precise mathematical notation leads to multiple interpretations, understanding fractions, percentages, ratios, and proportions is key to solving problems accurately and confidently. Mastering these fundamental concepts provides a solid foundation for tackling more complex mathematical challenges and practical applications in various fields. Remember to always strive for clarity and precision in your mathematical expression to avoid ambiguity and ensure accurate results. The ability to interpret mathematical language correctly is as important as the ability to perform the calculations themselves. This ability makes you a more astute problem-solver and allows for a better understanding of the world around you.
Latest Posts
Latest Posts
-
Musical Instruments Starting With E
Sep 23, 2025
-
160 Cm To Feet Inches
Sep 23, 2025
-
Which Country Code Is 66
Sep 23, 2025
-
How Do You Spell Shaun
Sep 23, 2025
-
404 Is What Area Code
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.