Prime Factor Tree For 198
sportsmenna
Sep 20, 2025 · 6 min read
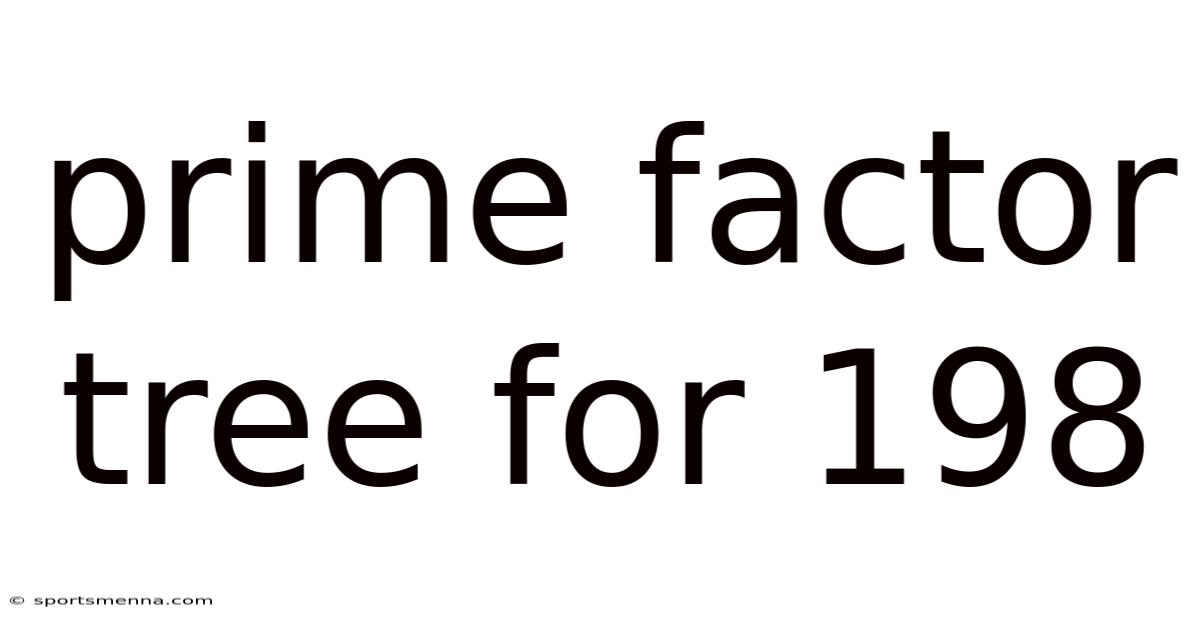
Table of Contents
Decomposing 198: A Deep Dive into Prime Factorization and Prime Factor Trees
Finding the prime factorization of a number might seem like a dry mathematical exercise, but it's a fundamental concept with far-reaching applications in algebra, cryptography, and even computer science. This article will guide you through the process of finding the prime factorization of 198 using a prime factor tree, explaining the underlying concepts in a clear and engaging way. We'll explore what prime numbers are, delve into the method of prime factorization, and answer common questions along the way. By the end, you’ll not only understand the prime factorization of 198 but also gain a solid understanding of this crucial mathematical technique.
What are Prime Numbers?
Before we embark on our journey to decompose 198, let's define our key players: prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it cannot be divided evenly by any other whole number without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number. Understanding prime numbers is crucial to understanding prime factorization.
Understanding Prime Factorization
Prime factorization is the process of breaking down a composite number (a number that is not prime) into its prime factors. Every composite number can be uniquely expressed as a product of prime numbers. This unique representation is known as the fundamental theorem of arithmetic. For instance, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). This means that 12 can only be constructed by multiplying these specific prime numbers together.
Constructing the Prime Factor Tree for 198
Now, let's tackle the prime factorization of 198 using the prime factor tree method. This is a visual method that makes the process easier to follow.
-
Start with the number: Begin by writing down the number 198 at the top of your tree.
-
Find the smallest prime factor: Look for the smallest prime number that divides 198 evenly. In this case, it's 2. Divide 198 by 2, which gives you 99.
-
Branch out: Draw two branches from 198, one leading to 2 and the other leading to 99.
-
Continue the process: Now, focus on 99. The smallest prime number that divides 99 evenly is 3. Divide 99 by 3 to get 33. Draw two branches from 99, one leading to 3 and the other to 33.
-
Repeat until you reach prime numbers: Continue this process with 33. The smallest prime factor of 33 is 3. Divide 33 by 3, giving you 11. Draw two branches from 33, one leading to 3 and the other to 11.
-
End with prime numbers: Notice that 11 is a prime number. This means we've reached the end of our branching.
Your completed prime factor tree for 198 should look like this:
198
/ \
2 99
/ \
3 33
/ \
3 11
- Write the prime factorization: Finally, list all the prime numbers at the end of each branch. In this case, they are 2, 3, 3, and 11. Therefore, the prime factorization of 198 is 2 x 3 x 3 x 11, or 2 x 3² x 11.
Alternative Methods for Prime Factorization
While the prime factor tree is a visually appealing and intuitive method, there are other ways to find the prime factorization of a number. One common alternative is to use repeated division. This method involves repeatedly dividing the number by the smallest prime number that divides it evenly until you reach 1.
Let's apply this method to 198:
- Divide 198 by 2: 198 / 2 = 99
- Divide 99 by 3: 99 / 3 = 33
- Divide 33 by 3: 33 / 3 = 11
- Divide 11 by 11: 11 / 11 = 1
The prime factors are the divisors used in each step: 2, 3, 3, and 11. This confirms our result from the prime factor tree method.
The Significance of Prime Factorization
The prime factorization of a number may seem like a simple mathematical exercise, but its applications extend far beyond the classroom. Here are some examples:
-
Simplifying Fractions: Prime factorization is essential for simplifying fractions to their lowest terms. By finding the prime factors of the numerator and denominator, you can identify common factors that can be canceled out.
-
Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization is the most efficient way to find the LCM and GCD of two or more numbers. The LCM is the smallest number that is a multiple of all the given numbers, while the GCD is the largest number that divides all the given numbers without leaving a remainder.
-
Cryptography: Prime factorization plays a crucial role in modern cryptography, particularly in RSA encryption. RSA relies on the difficulty of factoring very large numbers into their prime factors. This difficulty makes it computationally infeasible to break the encryption.
-
Abstract Algebra: Prime factorization is a fundamental concept in abstract algebra, which deals with more general algebraic structures.
-
Number Theory: Prime numbers and their properties are a central topic in number theory, a branch of mathematics concerned with the properties of integers.
Frequently Asked Questions (FAQ)
Q: Why is the prime factorization of a number unique?
A: The uniqueness of prime factorization is guaranteed by the fundamental theorem of arithmetic. This theorem states that every composite number can be expressed as a product of prime numbers in only one way, disregarding the order of the factors.
Q: Is there a limit to the size of prime numbers?
A: No, there is no largest prime number. There are infinitely many prime numbers. This fact was proven by Euclid over 2000 years ago.
Q: How can I check if a number is prime?
A: There are several ways to check if a number is prime. One method is to test for divisibility by all prime numbers less than the square root of the number. If it's not divisible by any of those primes, the number itself is prime. However, for very large numbers, more sophisticated primality tests are necessary.
Q: What if I make a mistake in my prime factor tree?
A: Don't worry if you make a mistake! The process is iterative. If you discover an error, simply retrace your steps and correct it. The beauty of the prime factor tree is that it allows for easy error correction.
Q: Are there any shortcuts for finding prime factors?
A: While there isn't a magic shortcut to instantly find all prime factors, recognizing divisibility rules for small prime numbers (2, 3, 5, 7, 11, etc.) can speed up the process. For example, if a number is even, you know it's divisible by 2. If the sum of its digits is divisible by 3, it's divisible by 3. These rules can help you quickly identify some of the prime factors.
Conclusion
Finding the prime factorization of 198, as we've demonstrated, is a straightforward process. Whether you use a prime factor tree or repeated division, the result remains the same: 2 x 3² x 11. Understanding this process isn't just about manipulating numbers; it's about grasping a fundamental concept that underlies many areas of mathematics and computer science. By mastering this skill, you're building a solid foundation for more advanced mathematical concepts. Remember, the key is practice. Try factoring other numbers using both methods to solidify your understanding. The more you practice, the quicker and more confident you'll become. So, grab a pencil and paper, and start exploring the fascinating world of prime numbers!
Latest Posts
Latest Posts
-
What Is 18st In Lbs
Sep 21, 2025
-
Meaning Of Ayan In Islam
Sep 21, 2025
-
Meaning Of Pay The Piper
Sep 21, 2025
-
Difference Between Deer And Reindeer
Sep 21, 2025
-
Merry Xmas In Italian Language
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 198 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.