Lcm Of 7 And 9
sportsmenna
Sep 21, 2025 · 6 min read
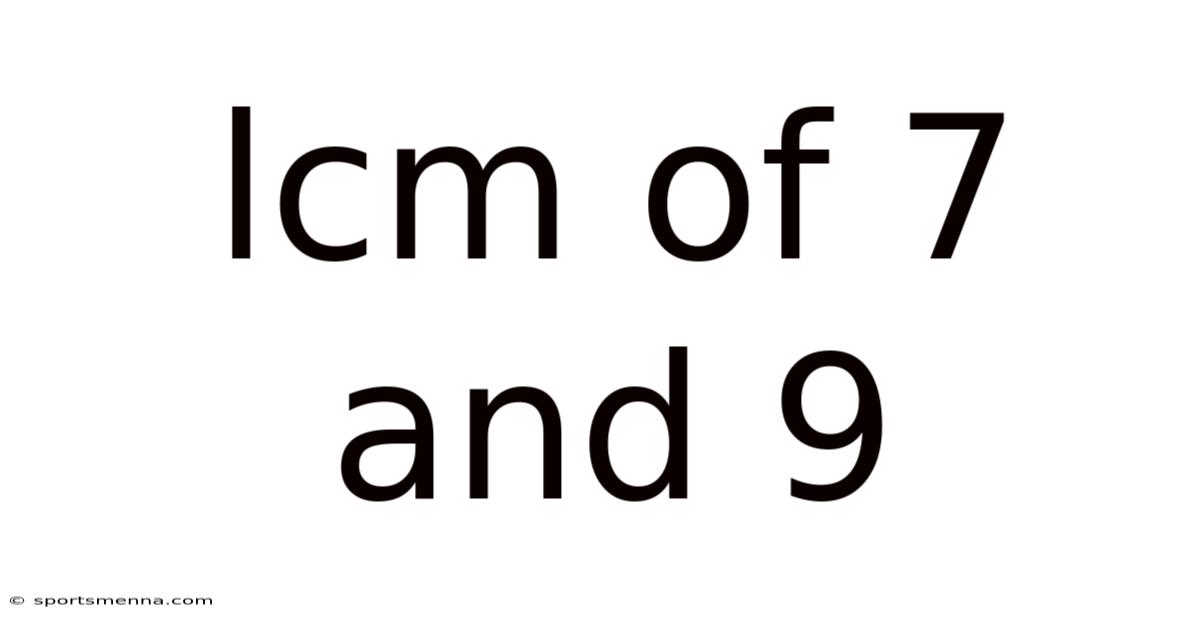
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 7 and 9, might seem like a simple arithmetic task. However, understanding the underlying concepts and exploring different methods for calculating the LCM provides a deeper understanding of number theory and its applications in various fields like mathematics, computer science, and even music. This comprehensive guide will explore several approaches to find the LCM of 7 and 9, explaining the logic behind each method and demonstrating its application with detailed examples. We'll also delve into the broader significance of LCMs and address frequently asked questions.
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both numbers divide into evenly. For instance, the multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70... and the multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72, 81... Notice that 63 is the smallest number that appears in both lists. Therefore, the LCM of 7 and 9 is 63.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 7 and 9. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
As you can see, the smallest number that appears in both lists is 63. Therefore, the LCM(7, 9) = 63.
This method is intuitive and easy to understand, but it becomes less efficient when dealing with larger numbers. Imagine trying to find the LCM of 127 and 257 using this method!
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 7: 7 (7 is a prime number, meaning its only divisors are 1 and itself)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together. In this case:
- The highest power of 3 is 3² = 9
- The highest power of 7 is 7¹ = 7
Therefore, LCM(7, 9) = 3² x 7 = 9 x 7 = 63
This method is more systematic and generally faster than the listing method, especially for larger numbers. It provides a deeper understanding of the number's structure and its relationship to prime numbers.
Method 3: Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. We can find the GCD using several methods, including the Euclidean algorithm.
Let's find the GCD of 7 and 9 using the Euclidean algorithm:
- Divide the larger number (9) by the smaller number (7): 9 ÷ 7 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (7) and the smaller number with the remainder (2): 7 ÷ 2 = 3 with a remainder of 1.
- Repeat: 2 ÷ 1 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 1. Therefore, GCD(7, 9) = 1.
Now, we can use the formula:
LCM(7, 9) = (7 x 9) / GCD(7, 9) = 63 / 1 = 63
This formula elegantly connects the LCM and GCD, demonstrating a fundamental relationship between these two concepts. It's a powerful tool for calculating LCMs, especially when dealing with larger numbers where prime factorization might become cumbersome.
The Significance of LCMs
The concept of the least common multiple finds applications in various areas:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. Finding the LCM of their arrival times helps determine when both buses will arrive simultaneously.
- Fraction Arithmetic: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator.
- Music Theory: The LCM is used in music theory to determine the least common period of two or more musical phrases with different rhythmic patterns.
- Computer Science: In areas like scheduling processes and managing memory allocation, the concept of LCM plays a significant role.
- Engineering: LCM is used in various engineering applications involving periodic events or signals.
Beyond Two Numbers: Finding the LCM of Multiple Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you would consider all prime factors from all the numbers involved, taking the highest power of each. For the formula-based approach, you would need to iteratively apply the GCD and LCM calculations for pairs of numbers until you reach the LCM of all numbers. For example, to find the LCM of 7, 9, and 10:
- Prime Factorization: 7 = 7, 9 = 3², 10 = 2 x 5
- LCM: 2 x 3² x 5 x 7 = 630
Frequently Asked Questions (FAQ)
Q1: What if the GCD of two numbers is the same as one of the numbers?
A1: If the GCD(a, b) = a (or b), it means 'a' is a factor of 'b'. In this case, the LCM(a, b) will simply be 'b' (or 'a').
Q2: Is there a limit to the size of numbers for which we can find the LCM?
A2: Theoretically, no. While the listing method becomes impractical for very large numbers, prime factorization and the GCD-based formula can be used to calculate the LCM of extremely large numbers using computational tools.
Q3: Can the LCM of two numbers be smaller than either of the numbers?
A3: No. The LCM is always greater than or equal to the larger of the two numbers. This is because the LCM must be a multiple of both numbers.
Q4: How can I check if my calculated LCM is correct?
A4: Verify that your calculated LCM is divisible by both original numbers without any remainder. You can also use an online LCM calculator to confirm your result.
Conclusion
Finding the least common multiple of 7 and 9, while seemingly simple, opens the door to a deeper understanding of number theory and its practical applications. We explored three different methods – listing multiples, prime factorization, and using the GCD – each with its own advantages and disadvantages. Understanding these methods provides a strong foundation for tackling more complex problems involving LCMs and GCDs, extending your mathematical capabilities beyond simple arithmetic calculations. Remember that the choice of method often depends on the size and nature of the numbers involved, but mastering all three methods ensures a comprehensive grasp of this important mathematical concept.
Latest Posts
Latest Posts
-
14 20 As A Percentage
Sep 21, 2025
-
What Is 63kg In Lbs
Sep 21, 2025
-
200 Degrees Celsius In Fahrenheit
Sep 21, 2025
-
Is 30 An Even Number
Sep 21, 2025
-
What Are Factors For 33
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.