Lcm Of 42 And 165
sportsmenna
Sep 24, 2025 · 6 min read
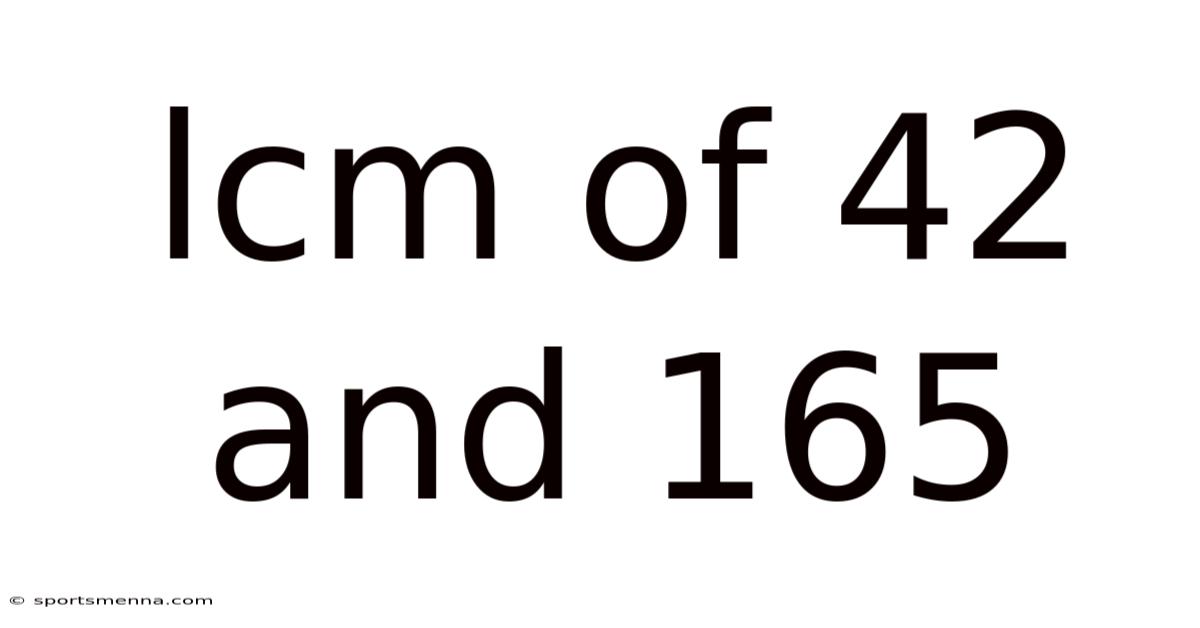
Table of Contents
Finding the Least Common Multiple (LCM) of 42 and 165: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a dry mathematical exercise, but understanding the concept unlocks a powerful tool for solving problems in various fields, from scheduling tasks to understanding rhythmic patterns in music. This article will guide you through different methods of calculating the LCM of 42 and 165, explaining the underlying principles and providing practical examples. We'll explore both the prime factorization method and the least common multiple formula, ensuring a thorough understanding of this fundamental mathematical concept. By the end, you'll be able to confidently calculate the LCM of any two numbers.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify what the least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept has practical applications in various real-world scenarios. Imagine you have two gears with 42 and 165 teeth, respectively. The LCM would represent the number of rotations needed for both gears to return to their starting positions simultaneously. Similarly, if you're planning events that repeat at intervals of 42 and 165 days, the LCM would determine when both events coincide again.
Method 1: Prime Factorization Method
This is arguably the most common and conceptually straightforward approach to finding the LCM. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply together to make the original number. Let's apply this method to find the LCM of 42 and 165:
Step 1: Prime Factorization of 42
We find the prime factors of 42 by repeatedly dividing by the smallest prime numbers until we reach 1:
- 42 ÷ 2 = 21
- 21 ÷ 3 = 7
- 7 ÷ 7 = 1
Therefore, the prime factorization of 42 is 2 × 3 × 7.
Step 2: Prime Factorization of 165
Now let's find the prime factors of 165:
- 165 ÷ 3 = 55
- 55 ÷ 5 = 11
- 11 ÷ 11 = 1
Therefore, the prime factorization of 165 is 3 × 5 × 11.
Step 3: Identifying Common and Unique Factors
Compare the prime factorizations of 42 and 165:
- 42 = 2 × 3 × 7
- 165 = 3 × 5 × 11
We see that they share one common prime factor: 3. The other factors (2, 7, 5, and 11) are unique to either 42 or 165.
Step 4: Calculating the LCM
To calculate the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(42, 165) = 2 × 3 × 5 × 7 × 11 = 2310
Therefore, the least common multiple of 42 and 165 is 2310.
Method 2: Using the Formula LCM(a, b) = (|a × b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the Euclidean algorithm to find the GCD efficiently.
Step 1: Finding the GCD of 42 and 165 using the Euclidean Algorithm
The Euclidean algorithm is an iterative process:
- Divide the larger number (165) by the smaller number (42) and find the remainder: 165 ÷ 42 = 3 with a remainder of 39.
- Replace the larger number with the smaller number (42) and the smaller number with the remainder (39).
- Repeat the process: 42 ÷ 39 = 1 with a remainder of 3.
- Repeat again: 39 ÷ 3 = 13 with a remainder of 0.
The last non-zero remainder is the GCD, which is 3.
Step 2: Applying the Formula
Now, we can use the formula:
LCM(a, b) = (|a × b|) / GCD(a, b)
LCM(42, 165) = (42 × 165) / 3 = 6930 / 3 = 2310
This method also yields the LCM of 42 and 165 as 2310.
Comparing the Two Methods
Both methods, prime factorization and using the GCD formula, are equally valid for finding the LCM. The prime factorization method is often preferred for its intuitive understanding, especially when dealing with smaller numbers. The GCD formula can be more efficient for larger numbers, as finding the GCD using the Euclidean algorithm is generally faster than performing extensive prime factorization for very large numbers.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond abstract mathematical exercises. Here are a few examples showcasing its real-world utility:
-
Scheduling: Imagine you have two tasks that need to be performed repeatedly. Task A is performed every 42 days, and Task B every 165 days. To find when both tasks will coincide again, you calculate the LCM(42, 165) = 2310. This means both tasks will be performed on the same day every 2310 days.
-
Music: In music theory, the LCM is used to determine when different rhythmic patterns will synchronize. If you have two rhythmic patterns with durations of 42 and 165 beats, the LCM(42, 165) = 2310 determines when the patterns will align again.
-
Manufacturing: In manufacturing processes involving multiple machines with different cycle times, the LCM helps in synchronizing operations and optimizing production efficiency.
-
Calendars: Determining when specific dates (e.g., birthdays, holidays) will fall on the same day of the week can involve the LCM concept, considering the number of days in a week and the cycle of the year.
Frequently Asked Questions (FAQ)
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined. The concept of LCM is only defined for positive integers.
Q: Can I use this method for more than two numbers?
A: Yes, you can extend the prime factorization method to find the LCM of more than two numbers. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to get the LCM.
Q: Is there a fastest way to find the LCM?
A: The efficiency of the method depends on the size of the numbers. For smaller numbers, prime factorization is often quick and intuitive. For larger numbers, the GCD formula combined with the Euclidean algorithm is usually more efficient.
Conclusion
Finding the least common multiple of two numbers, such as 42 and 165, is a fundamental mathematical concept with diverse applications. Both the prime factorization method and the GCD formula provide effective ways to calculate the LCM. Understanding these methods not only strengthens your mathematical skills but also equips you with a valuable tool applicable to various real-world problems involving cyclical events, scheduling, and rhythmic patterns. Remember that choosing the most efficient method depends on the context and the size of the numbers involved. With practice, calculating the LCM becomes a straightforward and valuable skill.
Latest Posts
Latest Posts
-
Convert Kw To Brake Horsepower
Sep 24, 2025
-
Things That Rhyme With Her
Sep 24, 2025
-
London Euston Tube To Victoria
Sep 24, 2025
-
Things That Come In 3
Sep 24, 2025
-
Miles From Ny To La
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 42 And 165 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.