Lcm Of 2 And 3
sportsmenna
Sep 21, 2025 · 6 min read
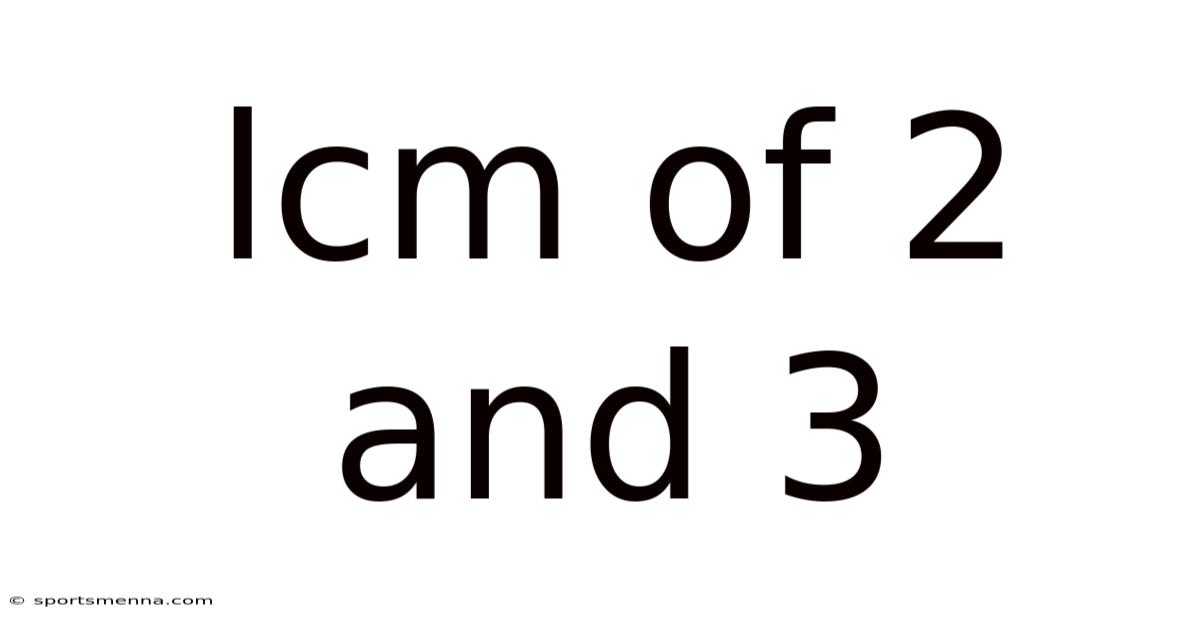
Table of Contents
Understanding the Least Common Multiple (LCM) of 2 and 3: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the concept behind it opens doors to more complex mathematical applications. This comprehensive guide will delve deep into calculating the LCM of 2 and 3, exploring various methods and illustrating its significance in different contexts. We'll move beyond a simple answer and uncover the underlying principles that govern this fundamental concept in number theory.
Introduction: What is the LCM?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers in the set as factors. For instance, the LCM of 2 and 3 is the smallest number that is a multiple of both 2 and 3. This seemingly simple concept forms the bedrock of many mathematical operations, particularly in areas like fractions, algebra, and even advanced topics like abstract algebra.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of small numbers like 2 and 3 is by listing their multiples. Let's do this:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
By comparing the lists, we can easily identify the smallest number that appears in both sequences: 6. Therefore, the LCM of 2 and 3 is 6.
Method 2: Prime Factorization
Prime factorization is a more robust method that works for larger numbers and multiple numbers. It involves expressing each number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime Factorization of 2: 2 (2 is a prime number itself)
- Prime Factorization of 3: 3 (3 is also a prime number)
Now, to find the LCM using prime factorization:
- Identify the highest power of each prime factor present in the factorizations. In this case, we have 2¹ and 3¹.
- Multiply these highest powers together: 2¹ x 3¹ = 6.
Thus, the LCM of 2 and 3 is again 6. This method is particularly useful when dealing with larger numbers where listing multiples becomes cumbersome.
Method 3: Using the Formula (for two numbers)
For two numbers, a and b, there's a handy formula that directly calculates the LCM:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where GCD stands for the greatest common divisor. The greatest common divisor is the largest number that divides both a and b without leaving a remainder.
- GCD(2, 3): The greatest common divisor of 2 and 3 is 1, as 1 is the only number that divides both 2 and 3.
- Applying the formula: LCM(2, 3) = (|2 * 3|) / 1 = 6 / 1 = 6.
This formula provides a direct and efficient way to compute the LCM, especially when the GCD is easily determined.
Method 4: Using the Euclidean Algorithm (for GCD)
If finding the GCD isn't immediately obvious (especially with larger numbers), the Euclidean algorithm is a highly efficient method. It works by repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's find the GCD of 2 and 3 using the Euclidean algorithm:
- Divide the larger number (3) by the smaller number (2): 3 = 2 * 1 + 1
- The remainder is 1. Since the remainder is not 0, we continue.
- Now, divide the previous divisor (2) by the remainder (1): 2 = 1 * 2 + 0
- The remainder is 0. The last non-zero remainder was 1, so the GCD(2, 3) = 1.
Now, we can use this GCD in the LCM formula from Method 3 to confirm that the LCM(2, 3) = 6.
The Significance of the LCM
Understanding the LCM extends beyond simple arithmetic exercises. Its applications are widespread:
-
Fractions: The LCM is crucial for adding and subtracting fractions. To add fractions with different denominators, you find the LCM of the denominators and then rewrite the fractions with this common denominator. For example, to add 1/2 and 1/3, you'd use the LCM of 2 and 3 (which is 6) to get 3/6 + 2/6 = 5/6.
-
Scheduling and Cyclical Events: Imagine two events that occur at different intervals. The LCM helps determine when both events will occur simultaneously. For example, if one event occurs every 2 days and another every 3 days, they will both occur together every 6 days (the LCM of 2 and 3). This is used in scheduling tasks, planning events, and even understanding astronomical cycles.
-
Modular Arithmetic: The LCM plays a critical role in modular arithmetic, a branch of number theory that deals with remainders after division. It helps solve congruences and other problems related to cyclic patterns.
-
Abstract Algebra: The concept of the least common multiple extends into abstract algebra, where it finds applications in ring theory and other advanced mathematical structures.
Addressing Common Questions (FAQ)
-
Q: Is the LCM always greater than or equal to the larger of the two numbers?
- A: Yes, the LCM of two numbers is always greater than or equal to the larger of the two numbers. This is because the LCM must be divisible by both numbers.
-
Q: What if I have more than two numbers? How do I find the LCM?
- A: For more than two numbers, the prime factorization method is most efficient. Find the prime factorization of each number, identify the highest power of each prime factor present, and multiply those highest powers together.
-
Q: What is the relationship between LCM and GCD?
- A: The LCM and GCD of two numbers are inversely related. As the GCD increases, the LCM decreases, and vice versa. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers (a x b = LCM(a,b) x GCD(a,b)).
-
Q: Are there any online tools or calculators for finding the LCM?
- A: Yes, many online calculators are available to compute the LCM of any set of numbers. However, understanding the underlying methods is crucial for deeper mathematical understanding.
Conclusion: Beyond the Numbers
While the LCM of 2 and 3 is simply 6, the journey to understanding how to arrive at that answer reveals much more than a basic arithmetic calculation. We’ve explored multiple methods, highlighting their strengths and applications. The importance of the LCM extends far beyond simple examples, touching upon various branches of mathematics and finding practical applications in diverse fields. By mastering the concept of the LCM and its associated methods, you not only strengthen your mathematical foundation but also develop a deeper appreciation for the interconnectedness of mathematical concepts. The ability to find the LCM is a stepping stone towards a more profound understanding of number theory and its wide-ranging applications in the world around us.
Latest Posts
Latest Posts
-
I Love You In Bengali
Sep 22, 2025
-
Good Morning In Igbo Language
Sep 22, 2025
-
Characters That Start With V
Sep 22, 2025
-
Net Price Vs Gross Price
Sep 22, 2025
-
What Is A Pure Metal
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.