Lcm Of 10 And 4
sportsmenna
Sep 22, 2025 · 6 min read
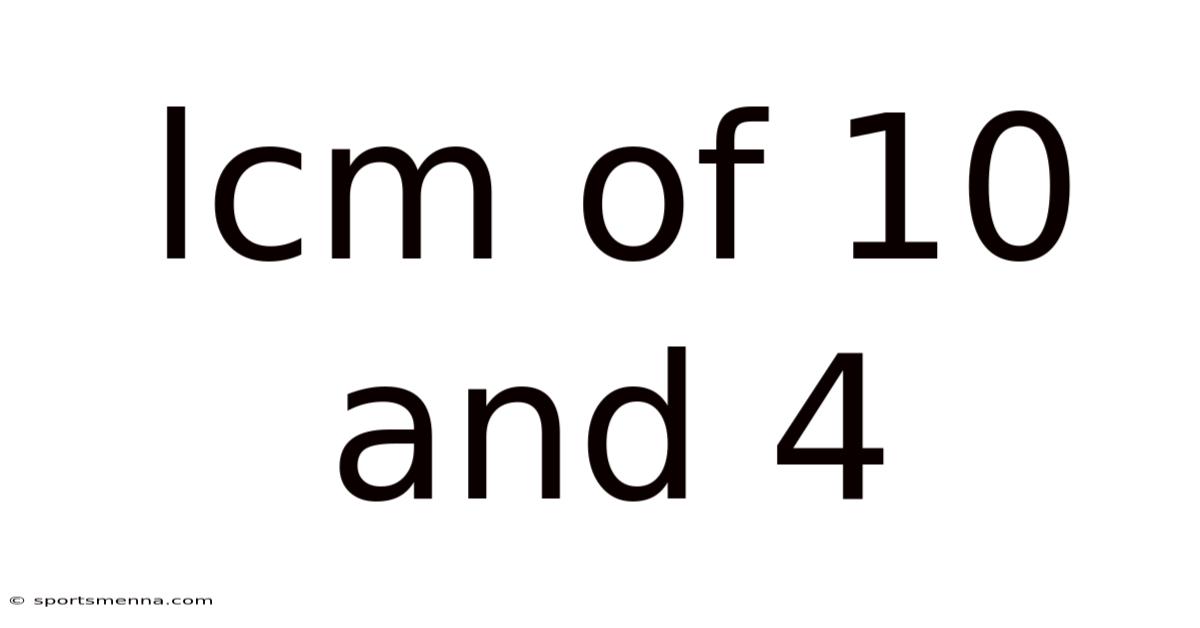
Table of Contents
Finding the Least Common Multiple (LCM) of 10 and 4: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving problems in algebra and beyond. This article will delve deep into determining the LCM of 10 and 4, explaining various methods, and exploring the underlying mathematical principles. We'll cover everything from basic definitions to advanced techniques, ensuring a comprehensive understanding for learners of all levels. Understanding LCMs is key to mastering fractions, ratios, and more advanced mathematical concepts.
What is the Least Common Multiple (LCM)?
Before we dive into calculating the LCM of 10 and 4, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the numbers in the set as factors. For example, if we consider the numbers 2 and 3, their LCM is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
The most straightforward method for finding the LCM, especially for smaller numbers like 10 and 4, is by listing their multiples. Let's do this:
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44...
By comparing the lists, we can identify the smallest number that appears in both sequences. In this case, it's 20. Therefore, the LCM of 10 and 4 is 20. This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
A more efficient and systematic approach, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime Factorization of 10: 10 = 2 x 5
- Prime Factorization of 4: 4 = 2 x 2 = 2²
Now, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 5 is 5¹ = 5
To find the LCM, we multiply these highest powers together:
LCM(10, 4) = 2² x 5 = 4 x 5 = 20
This method is more efficient than listing multiples, particularly when dealing with larger numbers or a greater number of integers. It provides a structured approach that ensures you find the LCM accurately.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the Greatest Common Divisor (GCD) are intimately related. The GCD is the largest number that divides both integers without leaving a remainder. There's a handy formula connecting the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two integers, and |a x b| represents the absolute value of their product.
Let's apply this to 10 and 4:
-
Finding the GCD of 10 and 4: The factors of 10 are 1, 2, 5, and 10. The factors of 4 are 1, 2, and 4. The greatest common factor is 2. Therefore, GCD(10, 4) = 2.
-
Applying the formula: LCM(10, 4) = (|10 x 4|) / GCD(10, 4) = 40 / 2 = 20
This method demonstrates the elegant relationship between LCM and GCD. It's a powerful technique, particularly useful when dealing with larger numbers where finding the GCD might be easier than directly finding the LCM.
Understanding the Concepts: Divisibility and Factors
Understanding the concepts of divisibility and factors is crucial for grasping the concept of LCM. A number is divisible by another number if it can be divided by that number without leaving a remainder. A factor is a number that divides another number evenly.
For example:
- 20 is divisible by 10 because 20 / 10 = 2 (no remainder).
- 10 is a factor of 20.
- 20 is also divisible by 4 because 20 / 4 = 5 (no remainder).
- 4 is a factor of 20.
The LCM is the smallest number that satisfies the divisibility rule for all the numbers in the set. This means it must have all the factors of those numbers within its own factorization.
Applications of LCM in Real-World Scenarios
The LCM isn't just a theoretical concept; it has practical applications in various areas:
-
Scheduling: Imagine two buses arrive at a stop at different intervals. One arrives every 10 minutes, and the other every 4 minutes. The LCM (20 minutes) determines when both buses will arrive at the stop simultaneously.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators allows you to find a common denominator, simplifying the calculation.
-
Measurement: When dealing with measurements using different units (e.g., converting inches to feet), the LCM can help you determine the smallest common unit for consistent measurement.
-
Project Management: In project management, if different tasks have varying completion times, the LCM can help determine when all tasks might be completed simultaneously.
Advanced Techniques for Finding LCM
For larger numbers or a greater number of numbers, more sophisticated algorithms are employed to efficiently find the LCM. These often leverage the prime factorization method or sophisticated variations of the GCD algorithm, like the Euclidean algorithm. These algorithms are beyond the scope of this introductory guide but are essential for efficient computations in computer science and advanced mathematics.
Frequently Asked Questions (FAQ)
-
Q: What if I have more than two numbers? A: The methods described above, particularly prime factorization, can be extended to find the LCM of more than two numbers. You would find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations.
-
Q: What if the numbers are negative? A: The LCM is always a positive integer. For negative numbers, simply find the LCM of their absolute values.
-
Q: Is there a limit to the size of numbers for which I can find the LCM? A: Theoretically, there's no limit. However, for extremely large numbers, computational limitations may arise, necessitating the use of advanced algorithms and computational tools.
-
Q: What is the relationship between LCM and GCD? A: The LCM and GCD are inversely related. As the GCD increases, the LCM decreases, and vice-versa. Their product is always equal to the product of the original two numbers.
-
Q: Can I use a calculator to find the LCM? A: Many scientific and graphing calculators have built-in functions to calculate the LCM of two or more numbers.
Conclusion
Finding the least common multiple (LCM) is a crucial skill in mathematics with wide-ranging applications. Understanding the different methods – listing multiples, prime factorization, and using the GCD – equips you with the tools to solve LCM problems efficiently. Whether dealing with small numbers or larger sets, mastering these techniques is fundamental for success in mathematics and related fields. Remember that the key is understanding the underlying principles of divisibility, factors, and the relationship between LCM and GCD. With practice, finding the LCM of any set of numbers will become second nature.
Latest Posts
Latest Posts
-
Significance Of The Number 16
Sep 22, 2025
-
Is A Tail A Limb
Sep 22, 2025
-
Meaning Of The Portugal Flag
Sep 22, 2025
-
I Love You In Swahili
Sep 22, 2025
-
How Much Does Cucumber Weigh
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.