Lcm 3 6 And 8
sportsmenna
Sep 19, 2025 · 6 min read
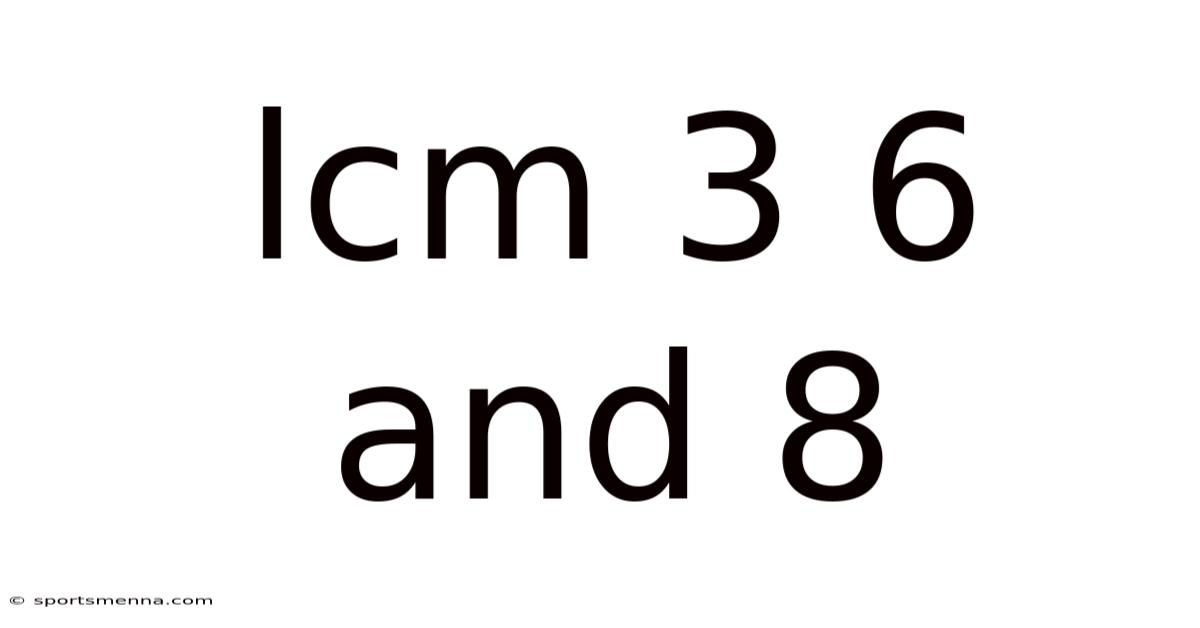
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 6, and 8: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple fraction arithmetic to complex scheduling problems. This article provides a comprehensive guide to calculating the LCM of 3, 6, and 8, explaining various methods and delving into the underlying mathematical principles. We'll explore different approaches, suitable for various levels of mathematical understanding, ensuring a clear and complete understanding of the concept. Understanding LCM is crucial for many areas, from simplifying fractions to solving real-world problems involving cyclical events.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. Finding the LCM is a crucial skill in arithmetic and algebra, particularly when working with fractions and simplifying expressions.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 8: 8, 16, 24, 32, 40...
By comparing the lists, we can see that the smallest number appearing in all three lists is 24. Therefore, the LCM of 3, 6, and 8 is 24. This method is effective for small numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the mathematical principles involved. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime Factorization of 3: 3 (3 is already a prime number)
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 8: 2 x 2 x 2 = 2³
Now, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
To find the LCM, we multiply these highest powers together: 2³ x 3 = 8 x 3 = 24
This method is more systematic and works well even with larger numbers. It clearly shows the relationship between the numbers and their prime factors, offering a more robust understanding than simply listing multiples.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
There's a relationship between the LCM and the greatest common divisor (GCD) of two numbers:
LCM(a, b) * GCD(a, b) = a * b
While this formula directly applies to only two numbers, we can extend it to three or more numbers by applying it iteratively. First, let's find the GCD of 3 and 6 using the Euclidean algorithm:
- 6 = 2 x 3 + 0
The GCD of 3 and 6 is 3. Now we can use the formula:
LCM(3, 6) * GCD(3, 6) = 3 * 6 LCM(3, 6) * 3 = 18 LCM(3, 6) = 6
Now, let's find the LCM of 6 and 8 using prime factorization or listing multiples:
- Multiples of 6: 6, 12, 18, 24, 30...
- Multiples of 8: 8, 16, 24, 32...
The LCM(6, 8) = 24
Therefore, the LCM of 3, 6, and 8 is 24. This iterative approach, while slightly more complex, demonstrates the interconnectedness of LCM and GCD.
Method 4: Using the Ladder Method (or Staircase Method)
This visual method is especially helpful for beginners. We arrange the numbers in a row and repeatedly divide them by their common prime factors until all numbers become 1.
2 | 3 6 8
2 | 3 3 4
2 | 3 3 2
3 | 3 3 1
| 1 1 1
We started by dividing by 2, then again by 2, then by 2, and finally by 3. The LCM is the product of all the divisors used: 2 x 2 x 2 x 3 = 24
This method offers a clear visual representation of the process, making it easier to follow, especially for those new to LCM calculations.
Explanation with Scientific Reasoning
The prime factorization method provides the most scientific explanation. Every integer greater than 1 can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). The LCM contains all the prime factors of the numbers involved, each raised to the highest power present in any of the numbers. This ensures that the resulting number is divisible by all the original numbers, and it's the smallest such number because we only include the highest powers of the prime factors. This is a fundamental concept in number theory.
Real-World Applications of LCM
Understanding LCM extends beyond abstract mathematical exercises. It has numerous practical applications:
- Scheduling: Imagine two buses that depart from the same station at different intervals. The LCM determines when they will depart simultaneously again. Similarly, it's used for scheduling events that repeat at different intervals.
- Fraction Addition and Subtraction: Finding a common denominator for fractions involves calculating the LCM of the denominators. This is essential for performing arithmetic operations on fractions.
- Gear Ratios: In mechanical engineering, LCM plays a vital role in determining gear ratios and synchronizing movements in machinery.
- Project Management: In project planning, LCM can help synchronize tasks that have different cycle times.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors?
A: If the numbers have no common factors (their GCD is 1), then their LCM is simply the product of the numbers. For example, the LCM of 5 and 7 is 35 (5 x 7).
Q: Can I use a calculator to find the LCM?
A: Yes, many scientific calculators have a built-in function to calculate the LCM. However, understanding the methods outlined above is crucial for grasping the underlying mathematical concepts.
Q: Is there a formula for finding the LCM of more than two numbers?
A: There isn't a single, compact formula like the one relating LCM and GCD for two numbers. However, you can extend the prime factorization method or the iterative GCD approach to find the LCM of any number of integers. The ladder method also extends easily to multiple numbers.
Q: Why is the LCM important in simplifying fractions?
A: When adding or subtracting fractions, you need a common denominator. The LCM of the denominators provides the smallest common denominator, simplifying the calculation and resulting in the simplest form of the answer.
Conclusion
Finding the LCM of 3, 6, and 8, as demonstrated using various methods, highlights the importance of understanding fundamental mathematical concepts. While listing multiples works well for small numbers, prime factorization provides a more powerful and efficient method, especially when dealing with larger integers. The relationship between LCM and GCD, and the ladder method offer alternative approaches providing different perspectives on the same fundamental concept. Regardless of the method chosen, the LCM of 3, 6, and 8 remains consistently 24. Understanding the LCM isn't just about solving mathematical problems; it's about understanding the underlying structure of numbers and their application in various real-world scenarios. Mastering this concept lays a solid foundation for further mathematical exploration and problem-solving.
Latest Posts
Latest Posts
-
18 Cm Converted To Inches
Sep 19, 2025
-
Gcf Of 12 And 15
Sep 19, 2025
-
How Long Are Church Services
Sep 19, 2025
-
1 16 As A Percentage
Sep 19, 2025
-
Flock Of Quails Is Called
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Lcm 3 6 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.