First Twenty Digits Of Pi
sportsmenna
Sep 23, 2025 · 7 min read
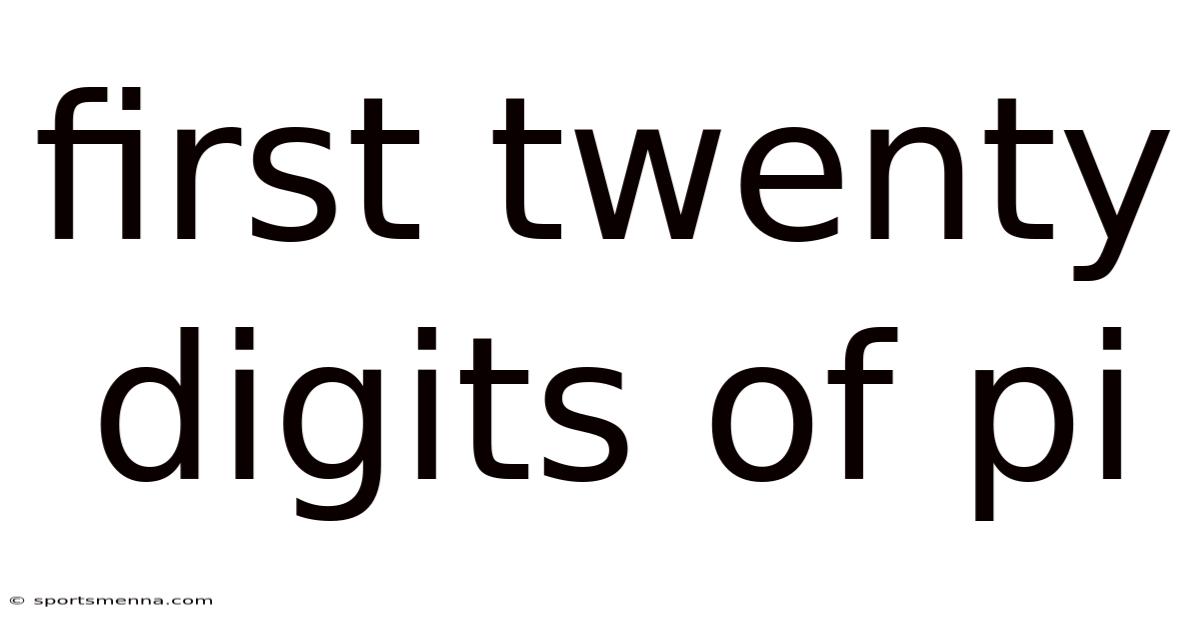
Table of Contents
The Enchanting First Twenty Digits of Pi: A Deep Dive into the Circle Constant
Pi (π), the ratio of a circle's circumference to its diameter, is a mathematical constant that has captivated mathematicians and enthusiasts for millennia. Its seemingly endless, non-repeating decimal expansion is a testament to the infinite complexity hidden within seemingly simple geometric shapes. This article delves into the first twenty digits of pi – 3.14159265358979323846 – exploring their significance, the methods used to calculate them, and the broader implications of this fascinating number. We'll uncover the history behind pi's computation, address common misconceptions, and delve into the beauty of its seemingly random sequence.
A Brief History of Pi's Calculation: From Ancient Civilizations to Supercomputers
The pursuit of pi's digits has been a long and arduous journey, spanning centuries and continents. Ancient civilizations, including the Babylonians and Egyptians, made early approximations, recognizing the constant relationship between a circle's circumference and diameter. The Babylonians, around 2000 BC, approximated pi as 3.125, while the Egyptians, around 1650 BC, used a value closer to 3.16.
Archimedes, the renowned Greek mathematician, significantly advanced the calculation of pi in the 3rd century BC. He employed a method of exhaustion, using polygons inscribed and circumscribed around a circle to progressively refine the approximation. His method yielded a value of pi between 3.1408 and 3.1429, a remarkable achievement for its time.
Over the centuries, mathematicians continued to refine the calculation of pi. The development of calculus in the 17th century opened up new avenues, leading to more efficient methods for computing its digits. Infinite series, like the Leibniz formula for π, provided a way to express pi as the sum of an infinite number of terms. However, these early methods were computationally intensive, requiring significant manual effort.
The advent of computers revolutionized pi calculation. The ability to perform billions of calculations per second allowed mathematicians to compute trillions of digits of pi. Algorithms like the Chudnovsky algorithm, which is significantly faster than previous methods, are now used to calculate pi to unimaginable precision. Today, we can calculate trillions of digits, far exceeding the practical needs of any scientific or engineering application. The calculation of pi serves as a benchmark for computational power and algorithmic efficiency.
The Significance of the First Twenty Digits: Precision in Practice
The first twenty digits of pi – 3.14159265358979323846 – provide an incredibly accurate representation for most practical applications. For everyday purposes, even using just 3.14 (or 22/7 for a simple fraction approximation) is often sufficient. However, the more digits we use, the greater the accuracy we achieve.
In engineering and scientific calculations, the required precision varies greatly depending on the application. For example, calculating the circumference of the Earth might only require a few decimal places of pi, while determining the precise trajectory of a spacecraft requires a much higher level of accuracy. Even within the context of extremely precise calculations, the first twenty digits often suffice. The need for more digits typically arises only in highly specialized areas of mathematics and computing, often related to testing algorithms or exploring the inherent properties of pi itself.
Consider these examples:
-
Calculating the circumference of a circle: For a circle with a diameter of 1 kilometer, using the first twenty digits of pi would yield a circumference accurate to within a fraction of a millimeter. This level of precision is far beyond what is typically needed in most real-world applications.
-
Calculating the area of a circle: Similarly, calculating the area of a circle using the first twenty digits would result in exceptionally high accuracy.
-
Scientific simulations: In simulations that involve circular or spherical objects, such as modeling planetary orbits or fluid dynamics, using a sufficient number of digits of pi ensures accurate results. However, even in complex simulations, the first twenty digits often provide accuracy exceeding practical requirements.
Beyond Practicality: The Mathematical Beauty of Pi's Digits
The significance of pi extends beyond its practical applications. The seemingly random sequence of its digits is a source of fascination for mathematicians. The distribution of digits appears to be random, with each digit appearing with roughly equal frequency. However, proving this randomness rigorously remains an open problem in mathematics.
The study of pi's digits has led to the development of new mathematical tools and techniques. The quest for more digits has pushed the boundaries of computational power and algorithmic efficiency, leading to advancements in computer science and numerical analysis.
Furthermore, pi's infinite and non-repeating decimal expansion reflects a fundamental property of irrational and transcendental numbers. It highlights the inherent complexity and beauty within seemingly simple mathematical concepts.
Common Misconceptions about Pi
Several misconceptions surround pi, many stemming from its seemingly mysterious nature. Let's clarify some of these:
-
Pi is exactly 22/7: This is a common approximation, but it is not the exact value of pi. 22/7 provides a reasonably close approximation, but it is only accurate to a few decimal places.
-
Pi ends after a certain number of digits: Pi's decimal expansion is infinite and non-repeating. It continues indefinitely without ever settling into a repeating pattern.
-
Pi has been completely calculated: While trillions of digits of pi have been calculated, its decimal expansion is infinite. We can never fully "calculate" pi in the sense of determining all its digits. The calculation is an ongoing process, pushing the boundaries of computational power.
-
Pi is only relevant to circles: While pi is intimately linked to circles, its applications extend far beyond geometry. It appears in many areas of mathematics, physics, and engineering, often in unexpected contexts.
Calculating Pi: A Glimpse into the Methods
While the actual computations are extremely complex and require advanced mathematical knowledge and sophisticated software, let's briefly touch upon some of the methods used to calculate pi's digits:
-
Infinite Series: These methods express pi as the sum of an infinite series of terms. The Leibniz formula is a classic example, although it converges to pi relatively slowly. More efficient series, such as the Ramanujan-type formulas and the Chudnovsky algorithm, are used for modern high-precision calculations.
-
Monte Carlo Methods: These probabilistic methods use random sampling to estimate pi. Imagine throwing darts randomly at a square that contains a circle. The ratio of darts landing within the circle to the total number of darts thrown approximates pi. This is a conceptually simple method, but it requires a vast number of iterations for high accuracy.
-
Spigot Algorithms: These algorithms allow for the calculation of individual digits of pi without needing to calculate the preceding digits. This is useful when only a specific range of digits is needed.
Frequently Asked Questions (FAQ)
-
Why is pi so important? Pi is fundamental to mathematics and science because it represents the ratio between a circle's circumference and its diameter, a relationship crucial in countless applications. Its transcendental nature makes it a rich subject of mathematical study.
-
What is the practical limit to the number of digits of pi needed? The practical limit depends heavily on the application. For most engineering and scientific purposes, a few dozen digits are far more than sufficient. High-precision calculations in specialized fields might require many more, but the need rarely exceeds several hundred digits.
-
Can we ever find the "last" digit of pi? No, the decimal expansion of pi is infinite and non-repeating. There is no "last" digit.
-
What are some interesting facts about pi? Pi appears in many unexpected places in mathematics and physics, beyond its connection to circles. It is also irrational (cannot be expressed as a fraction of two integers) and transcendental (not the root of any non-zero polynomial with rational coefficients).
-
Are there any patterns in the digits of pi? While the distribution of digits appears random, the presence of any specific patterns within the sequence is an ongoing area of research and debate.
Conclusion: The Enduring Allure of Pi
The first twenty digits of pi, while a small fraction of its infinite expansion, represent a significant milestone in humanity's understanding of this remarkable constant. Their calculation is a testament to our intellectual curiosity and our relentless pursuit of mathematical precision. From ancient approximations to the computational power of modern supercomputers, the journey to uncover pi's digits highlights the interwoven nature of mathematics, science, and technology. The seemingly endless sequence of digits continues to fascinate, challenging our understanding of randomness, infinity, and the beautiful complexities hidden within the simplest of geometric shapes. The quest to understand and calculate pi is far from over; it continues to inspire mathematicians, computer scientists, and enthusiasts worldwide. The first twenty digits, then, are not merely numbers; they are a gateway to a deeper appreciation of one of mathematics' most enduring mysteries.
Latest Posts
Latest Posts
-
97 Degrees F To C
Sep 23, 2025
-
1 Percent Inspiration 99 Perspiration
Sep 23, 2025
-
How Long Is 18 Centimeters
Sep 23, 2025
-
Jeff Chandler Cause Of Death
Sep 23, 2025
-
Charge Of A Silver Ion
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about First Twenty Digits Of Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.