9/5 As A Mixed Number
sportsmenna
Sep 24, 2025 · 5 min read
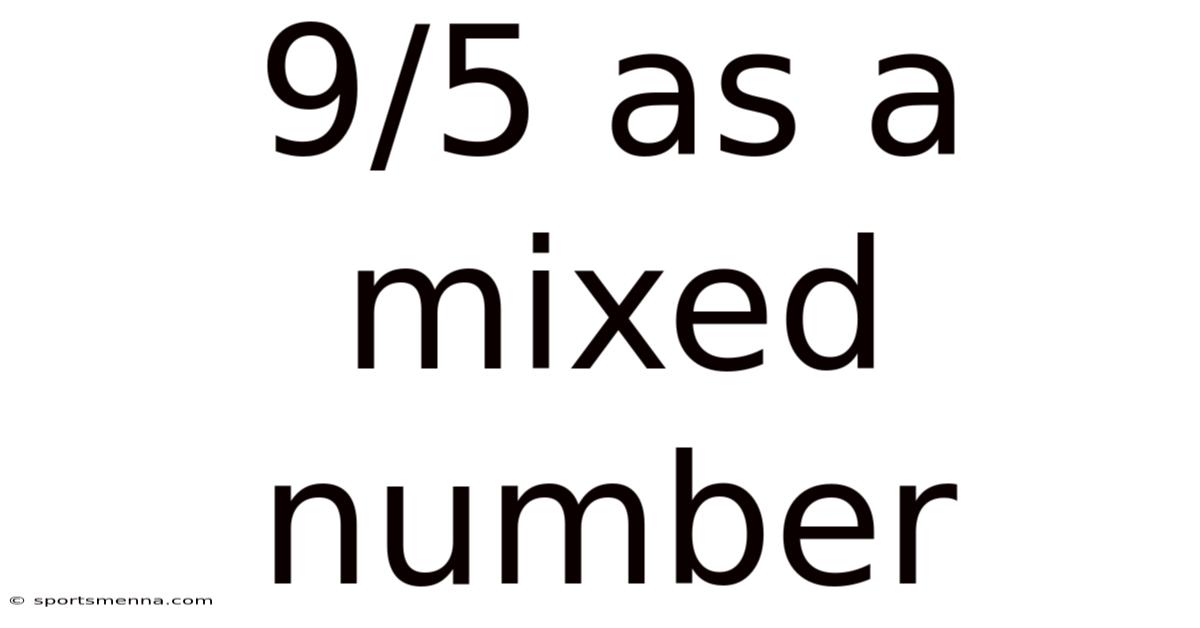
Table of Contents
Understanding 9/5 as a Mixed Number: A Comprehensive Guide
The fraction 9/5, representing nine-fifths, is an improper fraction because the numerator (9) is larger than the denominator (5). Improper fractions are often converted into mixed numbers for easier understanding and practical applications. This comprehensive guide will walk you through the process of converting 9/5 into a mixed number, explaining the underlying concepts, providing multiple methods, and addressing frequently asked questions. Understanding this conversion is fundamental to mastering fractions and tackling more advanced mathematical concepts.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than its denominator. For example, 1 ¾, 2 ⅓, and 3 ⅛ are all mixed numbers. They represent a quantity that's more than one whole unit but less than the next whole number. Converting improper fractions to mixed numbers makes it easier to visualize and compare quantities.
Converting 9/5 to a Mixed Number: The Division Method
The most common and straightforward method for converting an improper fraction to a mixed number involves division. Think of the fraction bar as representing division.
-
Divide the numerator by the denominator: Divide 9 by 5.
9 ÷ 5 = 1 with a remainder of 4
-
The quotient becomes the whole number: The result of the division (1) becomes the whole number part of the mixed number.
-
The remainder becomes the numerator: The remainder (4) becomes the numerator of the fraction part.
-
The denominator remains the same: The denominator (5) stays the same.
Therefore, 9/5 as a mixed number is 1 ⅘.
Visualizing the Conversion
Imagine you have nine fifths of a pizza. A whole pizza is divided into five equal slices. You have nine slices. You can make one complete pizza (five slices) and have four slices left over. This visually represents 1 ⅘ pizzas.
Converting 9/5 to a Mixed Number: The Subtraction Method
This method is less commonly used but offers a different perspective on the conversion process.
-
Identify how many times the denominator fits into the numerator: We know that 5 fits into 9 one time (5 x 1 = 5). This gives us our whole number.
-
Subtract the product from the numerator: Subtract the product (5) from the numerator (9): 9 - 5 = 4. This is our new numerator.
-
The denominator remains the same: The denominator stays as 5.
Therefore, we are left with 1 and ⅘, which combines to make the mixed number 1 ⅘.
Understanding the Equivalence
It's crucial to remember that 9/5 and 1 ⅘ are equivalent. They represent the same quantity. Converting between improper fractions and mixed numbers is simply a change in representation, not a change in value. This equivalence holds true for all improper fractions and their corresponding mixed numbers.
Practical Applications of Mixed Numbers
Mixed numbers are widely used in various everyday situations and across many academic disciplines:
-
Measurement: When measuring lengths, weights, or volumes, mixed numbers are often more convenient than improper fractions. For instance, it's more common to say a board is 2 3/4 feet long than to say it's 11/4 feet long.
-
Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities. For example, a recipe might call for 1 ½ cups of flour.
-
Time: Time is frequently expressed using mixed numbers. For example, 1 hour and 15 minutes can be expressed as 1 ¼ hours.
-
Construction and Engineering: Mixed numbers are essential in precise measurements and calculations within construction and engineering projects.
Further Exploration: Converting Other Improper Fractions
The methods explained above can be applied to any improper fraction. Let's look at a few examples:
-
11/3: Dividing 11 by 3 gives a quotient of 3 and a remainder of 2. Therefore, 11/3 = 3 ⅔.
-
17/6: Dividing 17 by 6 gives a quotient of 2 and a remainder of 5. Therefore, 17/6 = 2 ⅚.
-
25/8: Dividing 25 by 8 gives a quotient of 3 and a remainder of 1. Therefore, 25/8 = 3 ⅛.
Converting Mixed Numbers Back to Improper Fractions
The reverse process—converting a mixed number to an improper fraction—is also important. To do this:
-
Multiply the whole number by the denominator: For 1 ⅘, multiply 1 by 5 = 5.
-
Add the numerator: Add the result (5) to the numerator (4): 5 + 4 = 9.
-
Keep the denominator the same: The denominator remains 5.
Therefore, 1 ⅘ = 9/5. This confirms the equivalence we discussed earlier.
Frequently Asked Questions (FAQ)
Q: Why is it important to convert improper fractions to mixed numbers?
A: Converting improper fractions to mixed numbers improves readability and makes it easier to visualize quantities. It also simplifies calculations in many practical applications.
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, all improper fractions can be converted to mixed numbers.
Q: Are there other methods for converting improper fractions to mixed numbers besides division and subtraction?
A: While division and subtraction are the most common methods, other approaches involve visual representations or repeated subtraction. However, division remains the most efficient and widely used technique.
Q: What if the remainder is zero after the division?
A: If the remainder is zero, the improper fraction is already a whole number. For example, 10/5 = 2. There is no fractional part in the mixed number.
Q: How do I compare mixed numbers?
A: To compare mixed numbers, first compare the whole numbers. If the whole numbers are different, the larger whole number represents the larger mixed number. If the whole numbers are the same, compare the fractional parts.
Conclusion
Converting improper fractions to mixed numbers is a fundamental skill in mathematics. Understanding the process, whether through division or subtraction, empowers you to work confidently with fractions in various contexts. This conversion is not just a mathematical exercise; it's a tool that enhances your ability to solve practical problems and grasp quantitative concepts across diverse fields. Remember the key is to visualize the fractions and understand the underlying equivalence between the improper fraction and its mixed number representation. Mastering this skill will undoubtedly benefit you in your academic journey and beyond.
Latest Posts
Latest Posts
-
Positive Adjectives Beginning With Y
Sep 24, 2025
-
Cockney Rhyming Slang For House
Sep 24, 2025
-
60 Degrees Fahrenheit In Centigrade
Sep 24, 2025
-
Grandson Of Adam And Eve
Sep 24, 2025
-
P O Box 8743 Bellshill
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 9/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.