7 4 As A Decimal
sportsmenna
Sep 23, 2025 · 5 min read
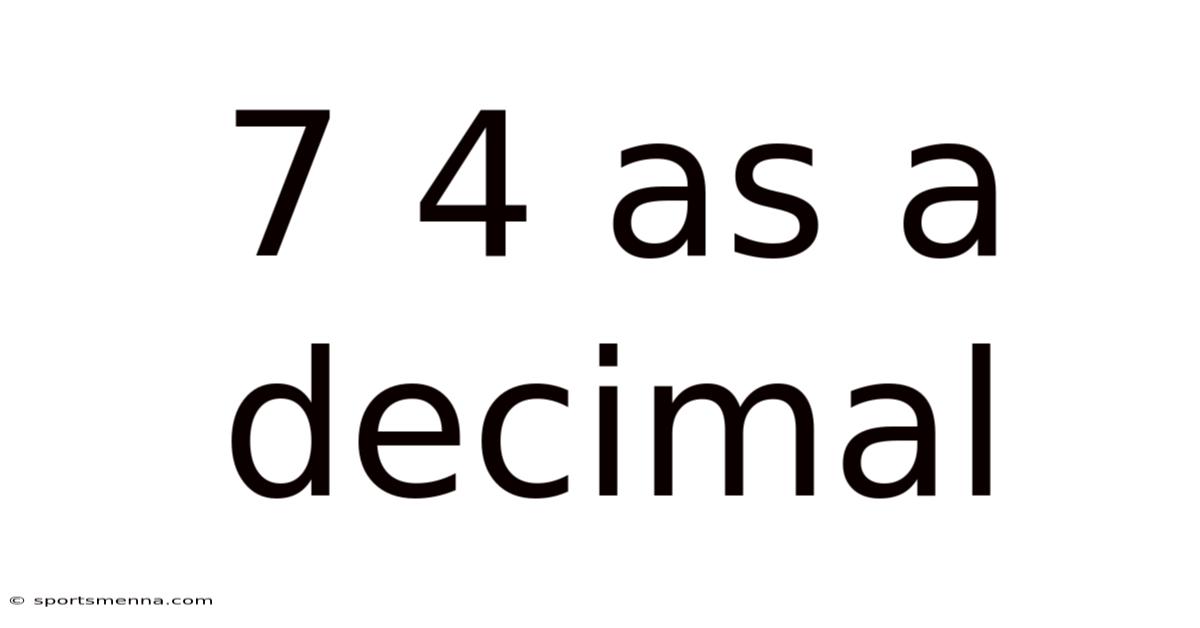
Table of Contents
7/4 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide will delve into the process of converting the fraction 7/4 into its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying concepts. We'll also cover frequently asked questions and address common misconceptions, ensuring a complete and readily understandable explanation.
Understanding Fractions and Decimals
Before we dive into converting 7/4, let's briefly review the fundamental concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
A decimal, on the other hand, represents a number using a base-ten system. The digits to the left of the decimal point represent whole numbers, while the digits to the right represent fractions of a whole, with each place value representing a power of ten (tenths, hundredths, thousandths, and so on).
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (4).
-
Set up the long division: Write 7 as the dividend (inside the long division symbol) and 4 as the divisor (outside the symbol).
-
Perform the division: 4 goes into 7 one time (4 x 1 = 4). Subtract 4 from 7, leaving a remainder of 3.
-
Add a decimal point and a zero: Add a decimal point to the quotient (the result of the division) and add a zero to the remainder. This allows us to continue the division process.
-
Continue dividing: 4 goes into 30 seven times (4 x 7 = 28). Subtract 28 from 30, leaving a remainder of 2.
-
Repeat the process: Add another zero to the remainder. 4 goes into 20 five times (4 x 5 = 20). The remainder is 0.
Therefore, 7/4 = 1.75
Method 2: Equivalent Fractions
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000). While not always possible directly, this method can be simpler for certain fractions.
In this case, we can't directly convert 4 into a power of 10. However, we can use the long division method (explained above) to arrive at the decimal value, which is the more efficient approach for this specific fraction.
Understanding the Result: 1.75
The decimal representation of 7/4 is 1.75. This means that 7/4 is equivalent to one whole unit and seventy-five hundredths of another unit. This can be visualized as one whole object and 75 out of 100 equal parts of another object.
Visual Representation
Imagine a pizza cut into four equal slices. 7/4 represents having seven of these slices. You would have one whole pizza (four slices) and three slices remaining, which represents ¾ of another pizza. This ¾ is equivalent to 0.75, thus giving us the total of 1.75.
Applications of Decimal Conversion
Converting fractions to decimals is essential in various real-world applications:
- Financial calculations: Calculating percentages, interest rates, and discounts often involves working with both fractions and decimals.
- Measurement: Many measuring tools (rulers, scales) use decimal systems, making conversion necessary for accurate measurements.
- Scientific calculations: Scientific measurements and data analysis frequently use decimal representations.
- Computer programming: Many programming languages use decimal representation for numerical data.
- Everyday life: From calculating tips in restaurants to splitting bills, understanding decimal equivalents is invaluable.
Beyond 7/4: Generalizing the Conversion Process
The methods outlined above can be applied to convert any fraction to its decimal equivalent. The long division method is particularly versatile and reliable for all types of fractions, whether they result in terminating decimals (like 7/4) or repeating decimals (like 1/3). The key is understanding the fundamental relationship between fractions and decimals: they represent different ways of expressing the same numerical value.
Frequently Asked Questions (FAQ)
Q: What if the fraction has a larger numerator than the denominator?
A: This indicates an improper fraction, meaning the fraction represents a value greater than 1. The long division method will still work, resulting in a decimal greater than 1.
Q: What if the decimal representation goes on forever (a repeating decimal)?
A: Some fractions, such as 1/3, have decimal representations that continue indefinitely with a repeating pattern (0.333...). These repeating decimals are often represented using a bar over the repeating digits (0.3̅).
Q: Are there other methods for converting fractions to decimals?
A: Yes, while long division and equivalent fractions are common methods, more advanced techniques exist, particularly for fractions with specific denominators. However, long division provides a reliable and broadly applicable approach.
Q: Why is it important to learn how to convert fractions to decimals?
A: This skill bridges the gap between two common representations of numbers, enabling easier calculations and problem-solving in diverse contexts. Many calculations are simpler with decimals, particularly those involving multiplication and division.
Q: Can I use a calculator to convert fractions to decimals?
A: Yes, calculators are a convenient tool for this conversion. However, understanding the underlying process is crucial for building a strong mathematical foundation.
Conclusion
Converting 7/4 to its decimal equivalent, 1.75, is a straightforward process that demonstrates the fundamental relationship between fractions and decimals. Mastering this conversion is a vital skill in mathematics, empowering you to tackle more complex problems and apply this knowledge to a wide array of real-world scenarios. Remember, practice is key! The more you practice converting fractions to decimals using different methods, the more comfortable and confident you will become with this essential mathematical concept. Understanding the 'why' behind the 'how' will solidify your grasp and build a solid mathematical foundation for future learning.
Latest Posts
Latest Posts
-
Purple On A Mood Necklace
Sep 24, 2025
-
Dobby The House Elf Death
Sep 24, 2025
-
What Is Factor Of 18
Sep 24, 2025
-
66 Position Ka Matlab Image
Sep 24, 2025
-
3 1kg In Pounds And Ounces
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.