7 16 As A Decimal
sportsmenna
Sep 21, 2025 · 5 min read
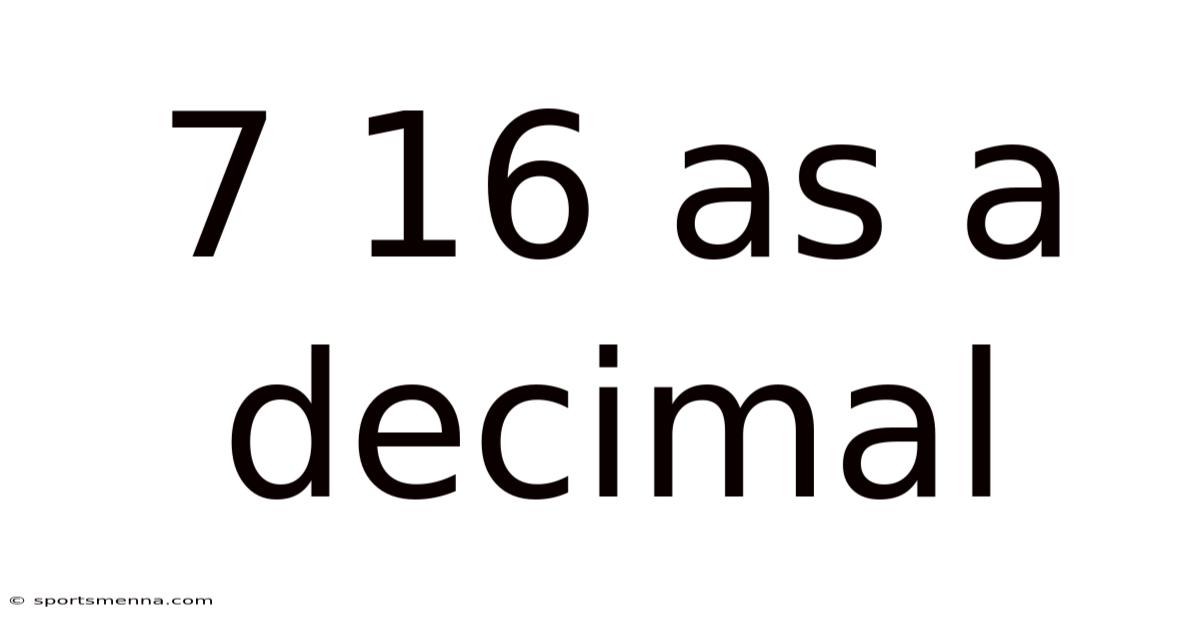
Table of Contents
Understanding 7/16 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, essential for various applications from everyday calculations to advanced scientific computations. This article provides a thorough explanation of how to convert the fraction 7/16 into a decimal, exploring different methods, underlying principles, and practical applications. We'll cover the process step-by-step, ensuring a clear understanding for all levels, from beginners to those seeking a more in-depth understanding of decimal representation. By the end, you'll not only know the decimal equivalent of 7/16 but also possess a strong foundation for converting other fractions.
Introduction to Fractions and Decimals
Before diving into the conversion of 7/16, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 7/16, 7 is the numerator and 16 is the denominator. This means we have 7 out of 16 equal parts of a whole.
A decimal, on the other hand, represents a number using a base-ten system. It uses a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, 0.5 represents five-tenths, and 0.25 represents twenty-five-hundredths.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (16).
-
Set up the division: Write 7 as the dividend (inside the division symbol) and 16 as the divisor (outside the division symbol). Since 7 is smaller than 16, add a decimal point after 7 and add a zero. This doesn't change the value of 7, but allows us to proceed with the division.
-
Perform the division: 16 goes into 70 four times (16 x 4 = 64). Write 4 above the 0 in the quotient. Subtract 64 from 70, leaving a remainder of 6.
-
Continue the division: Add another zero to the remainder (6) to get 60. 16 goes into 60 three times (16 x 3 = 48). Write 3 in the quotient after the decimal point. Subtract 48 from 60, leaving a remainder of 12.
-
Repeat the process: Add another zero to the remainder (12) to get 120. 16 goes into 120 seven times (16 x 7 = 112). Write 7 in the quotient. Subtract 112 from 120, leaving a remainder of 8.
-
Continue until termination or repetition: Add another zero to get 80. 16 goes into 80 five times (16 x 5 = 80). The remainder is 0. The division terminates.
Therefore, 7/16 = 0.4375
Method 2: Using Equivalent Fractions
Another approach involves converting the fraction 7/16 into an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.). While this is not always feasible, it can be a simpler method for certain fractions. Unfortunately, 16 cannot be easily converted to a power of 10. The prime factorization of 16 is 2⁴, and powers of 10 only contain prime factors of 2 and 5. Therefore, this method is less suitable for this specific fraction.
Method 3: Understanding Decimal Place Values
The decimal representation of 7/16 (0.4375) can be broken down into its place values:
- 0: Represents the whole number part.
- 4: Represents 4 tenths (4/10).
- 3: Represents 3 hundredths (3/100).
- 7: Represents 7 thousandths (7/1000).
- 5: Represents 5 ten-thousandths (5/10000).
Adding these values together (4/10 + 3/100 + 7/1000 + 5/10000) gives you 0.4375. This reinforces the understanding that decimals are simply a different way of expressing fractions with denominators that are powers of 10.
Practical Applications of Decimal Conversions
Converting fractions to decimals is crucial in various real-world applications:
-
Measurement and Engineering: In fields like engineering and construction, precise measurements are essential. Converting fractional measurements into decimals ensures accuracy in calculations and designs.
-
Finance: Calculations involving percentages, interest rates, and financial ratios often require converting fractions to decimals for accurate computations.
-
Data Analysis: In statistics and data analysis, representing data in decimal form is essential for calculations and visualizations.
-
Programming and Computing: Many programming languages and software applications require numerical data to be represented in decimal format for processing and calculations.
Frequently Asked Questions (FAQs)
Q: Are there other ways to convert 7/16 to a decimal?
A: Yes, you can use a calculator. Most calculators have a fraction-to-decimal conversion function. However, understanding the manual methods (like long division) provides a deeper understanding of the underlying mathematical principles.
Q: Why is it important to learn how to convert fractions to decimals manually?
A: While calculators are convenient, understanding the manual methods helps build a stronger foundation in mathematics. It promotes critical thinking and problem-solving skills, and it also allows you to perform calculations even when a calculator isn't readily available.
Q: What if the fraction results in a repeating decimal?
A: Some fractions, when converted to decimals, result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, the decimal representation is often rounded to a certain number of decimal places for practical purposes.
Q: Can all fractions be converted to terminating decimals?
A: No. Only fractions whose denominators have only 2 and/or 5 as prime factors can be converted to terminating decimals. Fractions with other prime factors in the denominator will result in repeating decimals.
Conclusion
Converting the fraction 7/16 to its decimal equivalent (0.4375) is a straightforward process, best accomplished using long division. Understanding this conversion is vital for numerous practical applications across various fields. This article has demonstrated the process step-by-step, explored alternative methods (where applicable), and highlighted the importance of mastering fraction-to-decimal conversions for a solid foundation in mathematics. Remember that understanding the underlying principles, beyond just obtaining the answer, is key to developing strong mathematical skills. This not only helps in solving immediate problems but also builds a robust foundation for tackling more complex mathematical concepts in the future.
Latest Posts
Latest Posts
-
Tattoo Of Cross On Finger
Sep 21, 2025
-
Instruments That Start With Y
Sep 21, 2025
-
Convert M To Square Meter
Sep 21, 2025
-
1m 83 Cm In Feet
Sep 21, 2025
-
What Is 25 Of 12
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.