7 10 As A Percentage
sportsmenna
Sep 24, 2025 · 5 min read
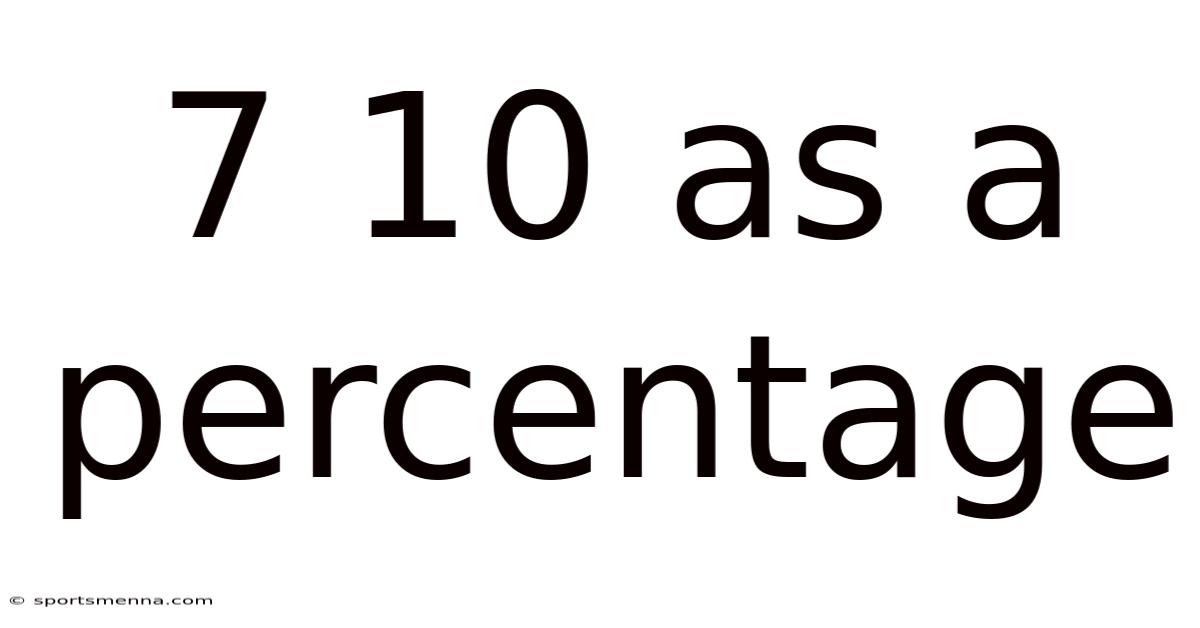
Table of Contents
7/10 as a Percentage: A Comprehensive Guide to Understanding Fractions, Decimals, and Percentages
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning numerous fields from everyday budgeting to advanced scientific calculations. This article provides a comprehensive guide to understanding how to express 7/10 as a percentage, exploring the underlying concepts and offering various methods for solving similar problems. We'll delve into the intricacies of fractions, decimals, and percentages, equipping you with the knowledge to confidently tackle these conversions. This guide is designed for learners of all levels, from those just beginning to grasp these concepts to those seeking a refresher or a deeper understanding.
Introduction: Fractions, Decimals, and Percentages – A Triad of Representation
Before diving into the specifics of 7/10, let's establish a solid foundation. These three mathematical representations – fractions, decimals, and percentages – all serve to express parts of a whole. They are simply different ways of expressing the same underlying value.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers: a numerator (top number) and a denominator (bottom number). The denominator indicates the total number of parts, while the numerator indicates the number of parts being considered. For example, 7/10 means 7 parts out of a total of 10 parts.
-
Decimals: Decimals are another way to represent parts of a whole, using a base-ten system. The decimal point separates the whole number part from the fractional part. Each digit to the right of the decimal point represents a decreasing power of 10 (tenths, hundredths, thousandths, and so on).
-
Percentages: Percentages express a fraction or decimal as a portion of 100. The percentage symbol (%) indicates that the number is a fraction of 100. For instance, 50% means 50 out of 100, or 50/100.
Method 1: Direct Conversion using the Percentage Formula
The most straightforward method for converting a fraction to a percentage is to use the fundamental percentage formula:
(Numerator / Denominator) x 100%
Let's apply this to 7/10:
(7 / 10) x 100% = 70%
Therefore, 7/10 is equivalent to 70%.
This method highlights the core relationship between fractions and percentages: the percentage represents the fraction scaled up to a denominator of 100.
Method 2: Converting the Fraction to a Decimal First
An alternative approach involves first converting the fraction to a decimal and then converting the decimal to a percentage.
-
Fraction to Decimal: To convert 7/10 to a decimal, simply divide the numerator (7) by the denominator (10):
7 ÷ 10 = 0.7
-
Decimal to Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.7 x 100% = 70%
Again, we arrive at the same result: 7/10 is equal to 70%. This method is particularly useful when dealing with fractions that don't easily simplify to a denominator of 100.
Method 3: Understanding the Concept of Proportionality
This method emphasizes the proportional relationship between the fraction and the percentage. Since a percentage is always out of 100, we can set up a proportion:
7/10 = x/100
To solve for x (the equivalent percentage), we can cross-multiply:
10x = 700
x = 700 / 10
x = 70
Therefore, 7/10 equals 70%. This approach reinforces the underlying mathematical principle of equivalent ratios.
Illustrative Examples: Extending the Concept
Let's explore a few more examples to solidify your understanding of these conversion methods.
-
Example 1: 3/5 as a percentage:
Using the formula: (3/5) x 100% = 60%
Converting to decimal first: 3 ÷ 5 = 0.6; 0.6 x 100% = 60%
-
Example 2: 1/4 as a percentage:
Using the formula: (1/4) x 100% = 25%
Converting to decimal first: 1 ÷ 4 = 0.25; 0.25 x 100% = 25%
-
Example 3: A more complex fraction – 17/25 as a percentage:
Using the formula: (17/25) x 100% = 68%
Converting to decimal first: 17 ÷ 25 = 0.68; 0.68 x 100% = 68%
These examples demonstrate the versatility and consistency of the different methods. Choose the method that feels most intuitive and comfortable for you.
The Significance of Understanding Percentages
The ability to convert fractions to percentages is crucial for various real-world applications:
- Financial Literacy: Calculating interest rates, discounts, taxes, and tips all involve percentage calculations.
- Data Analysis: Representing data in percentage form makes it easier to understand and compare proportions.
- Scientific Research: Percentages are frequently used to express experimental results and statistical data.
- Everyday Life: Understanding percentages helps in making informed decisions about shopping, budgeting, and more.
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand the relationship between fractions, decimals, and percentages?
A1: Understanding the interrelationship between these three forms allows for flexibility in calculations and problem-solving. Being able to seamlessly convert between them allows you to choose the most convenient format for a particular task.
Q2: Can I use a calculator for these conversions?
A2: Absolutely! Calculators can significantly simplify the process, especially when dealing with more complex fractions.
Q3: What if the fraction has a large denominator? Does the method change?
A3: No, the methods remain the same. The calculation might be more complex, but the underlying principles remain consistent. You can use a calculator to ease the division.
Q4: Are there any online tools or resources available to help with these conversions?
A4: Yes, numerous online calculators and educational websites offer tools to convert fractions to percentages and vice-versa.
Conclusion: Mastering Fraction-to-Percentage Conversions
Mastering the conversion of fractions to percentages is a valuable skill that enhances mathematical proficiency and opens doors to a deeper understanding of quantitative information. Whether you use the direct formula, the decimal conversion method, or the proportionality approach, the key is to understand the underlying principles connecting fractions, decimals, and percentages. Practice is crucial to build confidence and fluency in applying these methods. With consistent practice and a clear understanding of the concepts, you'll confidently navigate the world of fractions, decimals, and percentages. Remember, 7/10, 0.7, and 70% all represent the same value – just expressed differently. This understanding empowers you to tackle various mathematical challenges and confidently interpret data in diverse contexts.
Latest Posts
Latest Posts
-
What Is 81cm In Inches
Sep 24, 2025
-
0 3 Repeating As A Fraction
Sep 24, 2025
-
New Zealand To Australia Distance
Sep 24, 2025
-
How To Cite A Sermon
Sep 24, 2025
-
How Do U Spell Mischievous
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7 10 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.