6 10 As A Percent
sportsmenna
Sep 24, 2025 · 5 min read
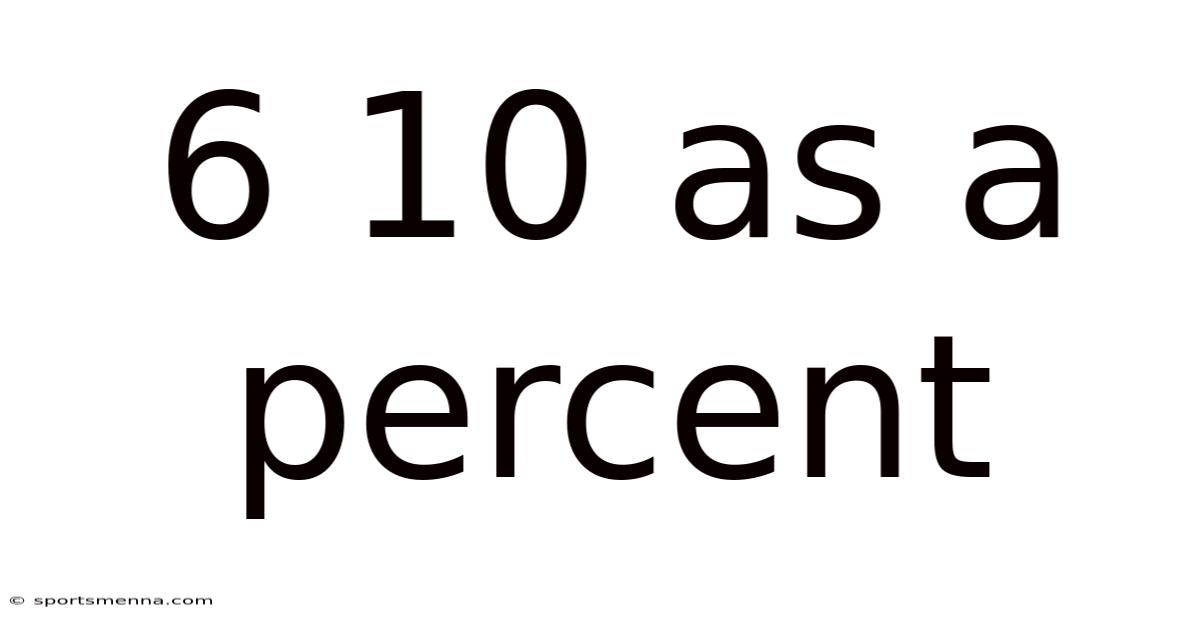
Table of Contents
Understanding 6/10 as a Percent: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from calculating grades to understanding financial data. This comprehensive guide will delve into the process of converting the fraction 6/10 into a percentage, explaining the underlying principles and providing practical examples. We'll explore different methods, address common misconceptions, and answer frequently asked questions to ensure a thorough understanding of this essential concept.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before we dive into converting 6/10 to a percentage, let's establish a firm understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 6/10, 6 is the numerator and 10 is the denominator. This signifies 6 out of 10 parts.
-
Decimal: A decimal represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals use a decimal point to separate the whole number from the fractional part. For instance, 0.6 is the decimal equivalent of 6/10.
-
Percentage: A percentage represents a fraction where the denominator is always 100. It indicates "per hundred" and is denoted by the symbol %. For example, 60% means 60 out of 100.
These three are interchangeable; you can convert one form into another. This interconnectivity is crucial for understanding mathematical concepts and solving real-world problems.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 6/10 into a percentage involves understanding that a percentage is simply a fraction with a denominator of 100. Therefore, we need to manipulate 6/10 to have a denominator of 100. This can be achieved by multiplying both the numerator and the denominator by the same number. Since 10 multiplied by 10 equals 100, we'll use 10 as our multiplier:
(6/10) * (10/10) = 60/100
Now that we have a fraction with a denominator of 100, we can easily express it as a percentage: 60/100 = 60%
Method 2: Converting to a Decimal First
An alternative method involves converting the fraction 6/10 into a decimal first, then converting the decimal into a percentage.
To convert 6/10 to a decimal, we simply divide the numerator (6) by the denominator (10):
6 ÷ 10 = 0.6
Now, to convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.6 * 100 = 60
Therefore, 0.6 is equivalent to 60%.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between fractions and percentages. We can set up a proportion:
6/10 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
10x = 600
Now, divide both sides by 10:
x = 60
Therefore, 6/10 is equal to 60%.
Visual Representation: Understanding the Concept
Imagine a pizza cut into 10 equal slices. If you eat 6 slices, you've eaten 6 out of 10 slices, or 6/10 of the pizza. This is the same as eating 60 out of 100 slices (if the pizza were cut into 100 slices), which is 60%. This visual representation helps solidify the understanding of the equivalence between the fraction, decimal, and percentage.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is essential in numerous real-world scenarios:
-
Academic Grades: If you score 6 out of 10 on a quiz, your grade is 60%.
-
Financial Calculations: Understanding percentages is critical for calculating interest rates, discounts, tax rates, and profit margins.
-
Data Analysis: Percentages are often used to represent proportions in data analysis and statistical reports.
-
Everyday Life: We encounter percentages regularly in sales, tips, surveys, and much more.
Common Misconceptions and How to Avoid Them
-
Confusing numerator and denominator: Remember that the numerator is the top number and the denominator is the bottom number. Incorrectly swapping these will lead to an inaccurate calculation.
-
Forgetting to multiply by 100: When converting a decimal to a percentage, remember to multiply the decimal by 100. This step is crucial for obtaining the correct percentage.
-
Not simplifying fractions: Before converting a fraction to a percentage, simplify the fraction to its lowest terms if possible. This simplifies the calculation. For example, converting 10/20 to a percentage is easier after simplifying it to 1/2.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, absolutely. Any fraction can be converted to a percentage by following the methods outlined above.
Q2: What if the denominator isn't a factor of 100?
A2: If the denominator isn't a factor of 100, you can still convert the fraction to a percentage by first converting it to a decimal and then multiplying by 100. Alternatively, you can use the proportion method.
Q3: How do I convert a percentage back to a fraction?
A3: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 60% becomes 60/100, which simplifies to 3/5.
Q4: Are there online calculators to help with this conversion?
A4: Yes, many online calculators are available that can quickly convert fractions to percentages and vice versa. However, understanding the underlying mathematical principles is crucial for solving problems independently.
Q5: What if the fraction is greater than 1?
A5: If the fraction is greater than 1 (improper fraction), convert it to a mixed number or an equivalent decimal, and then multiply by 100 to obtain the percentage. For instance, 11/10 = 1.1, which is 110%.
Conclusion: Mastering Percentage Conversions
Converting 6/10 to a percentage, which is 60%, is a straightforward process once you understand the relationship between fractions, decimals, and percentages. This guide has provided multiple methods for this conversion, explained the underlying principles, addressed common misconceptions, and answered frequently asked questions. Mastering percentage conversions is a valuable skill that will serve you well in various academic, professional, and everyday situations. By understanding these concepts, you’ll be better equipped to tackle more complex mathematical problems and gain a deeper understanding of numerical representations. Remember, consistent practice is key to developing proficiency in these essential mathematical skills.
Latest Posts
Latest Posts
-
Countries That End In Ia
Sep 24, 2025
-
Winner Winner Chicken Dinner Meaning
Sep 24, 2025
-
Things That Rhyme With Beach
Sep 24, 2025
-
47 Out Of 60 Percentage
Sep 24, 2025
-
Human And Dog Have Sex
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 6 10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.