5 8 Divided By 2
sportsmenna
Sep 22, 2025 · 6 min read
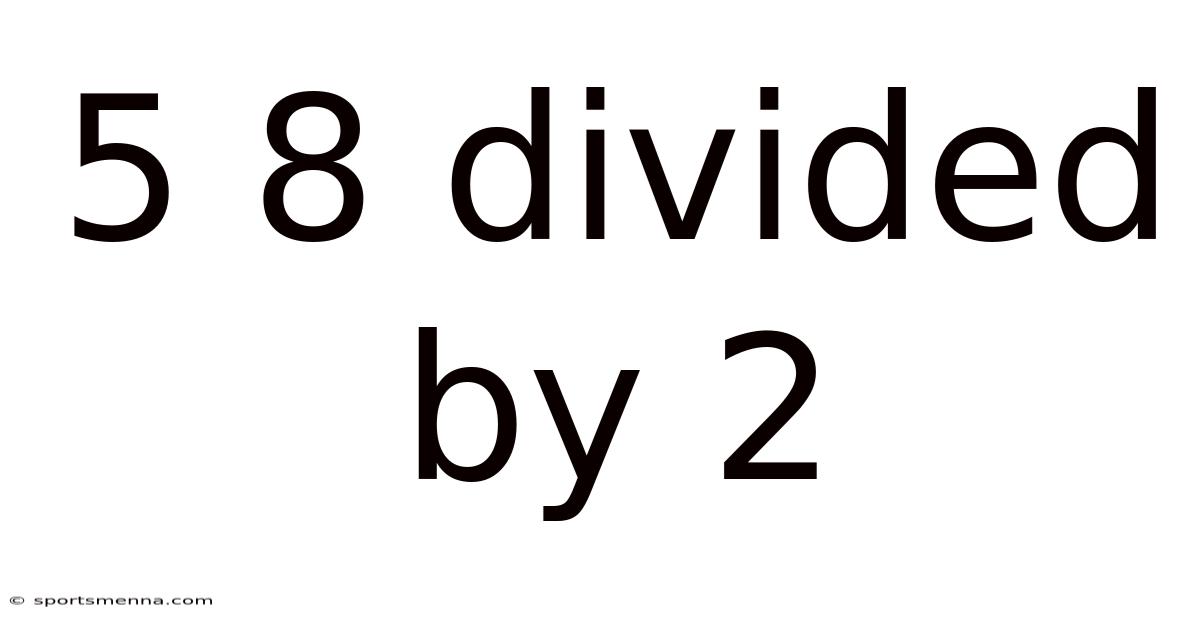
Table of Contents
Decoding 58 Divided by 2: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 58 divided by 2, delving far beyond the basic answer to uncover the underlying mathematical principles, various methods of solving the problem, and the broader applications of division in everyday life and advanced fields. Understanding division is fundamental to grasping more complex mathematical concepts, and this in-depth exploration will illuminate its significance. We'll examine different approaches, discuss the concept of remainders, and explore real-world examples to solidify your understanding.
Introduction: The Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts or groups. In the case of 58 divided by 2 (written as 58 ÷ 2, 58/2, or 2)⦋58), we're asking: "How many times does 2 fit into 58?" The answer, as we'll see through several methods, reveals a fundamental aspect of number theory and its practical applications.
Method 1: Long Division – The Classic Approach
Long division is a standard algorithm taught in schools to solve division problems, especially those involving larger numbers. Here's how to solve 58 ÷ 2 using long division:
-
Set up the problem: Write 58 inside the long division symbol (÷) with 2 outside.
-
Divide the tens digit: How many times does 2 go into 5? It goes in 2 times (2 x 2 = 4). Write the '2' above the '5' in the quotient (the answer).
-
Subtract: Subtract 4 from 5 (5 - 4 = 1).
-
Bring down the ones digit: Bring down the '8' from the dividend (58) next to the 1, making it 18.
-
Divide the ones digit: How many times does 2 go into 18? It goes in 9 times (2 x 9 = 18). Write the '9' next to the '2' in the quotient.
-
Subtract: Subtract 18 from 18 (18 - 18 = 0). There is no remainder.
Therefore, 58 ÷ 2 = 29.
Method 2: Repeated Subtraction – A Conceptual Approach
This method helps visualize the concept of division. It involves repeatedly subtracting the divisor (2) from the dividend (58) until you reach zero. The number of times you subtract represents the quotient.
- 58 - 2 = 56
- 56 - 2 = 54
- 54 - 2 = 52
- ...and so on.
While this method is effective for smaller numbers, it becomes cumbersome for larger ones. It's crucial, however, for understanding the core principle of division: repeated subtraction until the remainder is zero. Counting the number of subtractions will also lead to the answer of 29.
Method 3: Halving – A Quick and Efficient Method
Since we're dividing by 2, we can use the halving method – a shortcut for dividing by powers of 2. Simply divide the number in half repeatedly. For 58:
- 58 / 2 = 29
This method directly leads to the answer of 29. This highlights the efficiency of using shortcuts for certain types of division problems.
Understanding Remainders: When Division Doesn't Go Evenly
While 58 ÷ 2 results in a whole number, not all division problems yield such neat results. Sometimes, there's a remainder – a number left over after the division is complete. Let's consider an example: 59 ÷ 2.
Using long division:
- 2 goes into 5 twice (2 x 2 = 4). Subtract 4 from 5 to get 1.
- Bring down the 9. 2 goes into 19 nine times (2 x 9 = 18). Subtract 18 from 19 to get 1.
The quotient is 29, and the remainder is 1. This is often written as 29 R 1 or 29 + 1/2 (or 29.5 in decimal form). Understanding remainders is critical in various applications, from sharing items equally to calculating averages.
Real-World Applications of Division: From Everyday Life to Advanced Fields
Division is not just a classroom exercise; it's a vital tool used across many disciplines:
-
Everyday Life: Sharing equally among friends, calculating unit prices (price per item), figuring out travel time based on speed and distance, splitting bills, recipe scaling (adjusting ingredient quantities), and much more.
-
Engineering and Physics: Calculating stresses and strains in structures, determining velocities and accelerations, analyzing circuit currents, and designing mechanical systems.
-
Computer Science: Data structures, algorithm design, and cryptographic operations rely heavily on division. Hashing, a technique used to organize and store data, uses modulo operations (which involves division and remainders).
-
Finance: Calculating interest rates, amortization schedules (loan repayments), determining investment returns, and analyzing financial ratios.
-
Statistics: Calculating averages (means), standard deviations, and other statistical measures heavily involve division.
-
Chemistry: Stoichiometry, the calculation of reactant and product quantities in chemical reactions, relies significantly on division.
Beyond the Basics: Exploring More Complex Division Problems
While 58 ÷ 2 is relatively straightforward, the principles extend to far more complex problems:
-
Dividing by larger numbers: Understanding the long division algorithm allows you to tackle divisions with much larger divisors and dividends.
-
Dividing decimals: The process remains similar, but involves handling decimal points carefully.
-
Dividing fractions: Dividing by a fraction is equivalent to multiplying by its reciprocal.
-
Dividing integers (positive and negative numbers): Remember the rules for integer division: positive/positive = positive; negative/positive = negative; positive/negative = negative; negative/negative = positive.
Frequently Asked Questions (FAQs)
-
Q: What is the inverse operation of division?
A: Multiplication. Multiplying the quotient by the divisor gives you the dividend. For example, 29 x 2 = 58.
-
Q: Why is understanding remainders important?
A: Remainders show that a division didn't result in equal groups. In real-world scenarios, this means that there might be something left over, requiring additional consideration or adjustments.
-
Q: Are there different ways to represent division?
A: Yes. Besides the symbols ÷ and /, division can be represented using fractions (e.g., 58/2) or as a long division problem.
-
Q: What are some common mistakes to avoid when performing division?
A: Common mistakes include misplacing digits during long division, incorrect handling of decimal points, and neglecting to consider remainders when necessary.
Conclusion: The Enduring Importance of Division
This detailed exploration of 58 divided by 2 has moved beyond the simple answer of 29 to reveal the profound significance of division in mathematics and various practical applications. From the straightforward methods of solving the problem to the more nuanced concepts like remainders and the myriad ways division is used in different fields, we've seen that understanding this fundamental operation is key to a broader grasp of quantitative reasoning. The seemingly simple act of dividing 58 by 2 opens doors to a deeper understanding of numbers, their relationships, and their real-world implications. By mastering the concept of division, you equip yourself with a powerful tool for solving problems and understanding the world around you.
Latest Posts
Latest Posts
-
What Shapes Are The Strongest
Sep 22, 2025
-
Inverse Of Log On Calculator
Sep 22, 2025
-
50 Million Dollars To Inr
Sep 22, 2025
-
Tyre Pressure For Citroen C3
Sep 22, 2025
-
Good Morning Beautiful In French
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 8 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.