4 7 As A Percentage
sportsmenna
Sep 21, 2025 · 5 min read
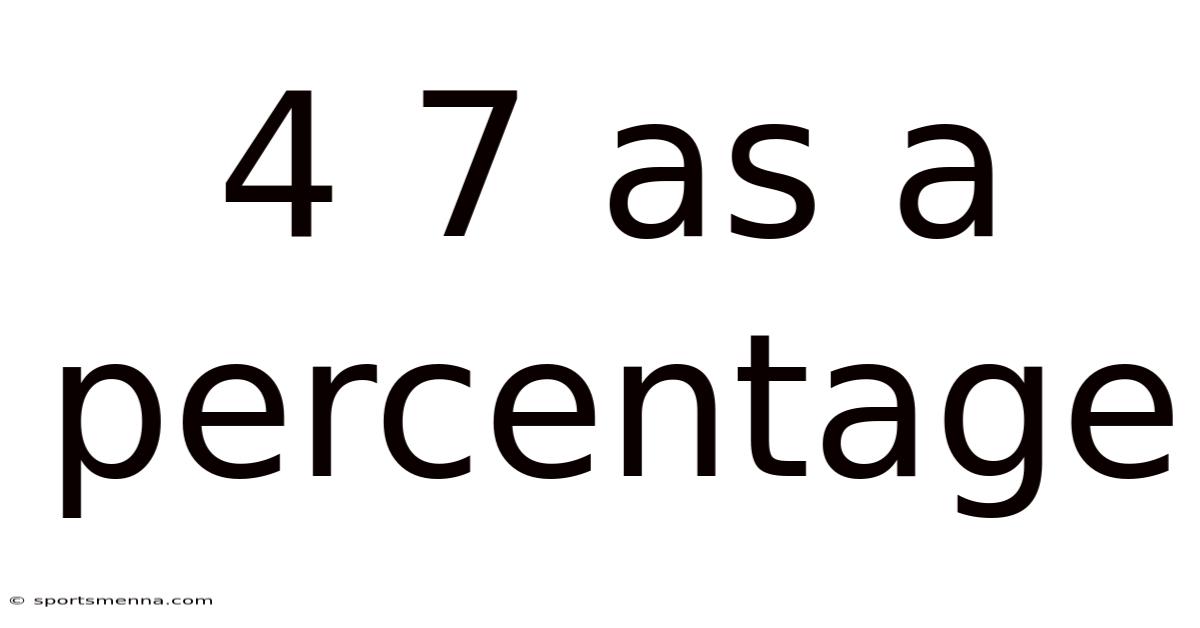
Table of Contents
Understanding 4/7 as a Percentage: A Comprehensive Guide
What is 4/7 as a percentage? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics with widespread applications in everyday life, from calculating discounts to understanding financial reports. This article will not only answer the question directly but also delve into the underlying principles, providing you with a robust understanding of the conversion process and its significance.
Introduction to Fractions, Decimals, and Percentages
Before we dive into converting 4/7 to a percentage, let's refresh our understanding of these core mathematical concepts.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For instance, in the fraction 4/7, 4 is the numerator and 7 is the denominator. This means we have 4 parts out of a total of 7 equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-10 system, with the decimal point separating the whole number part from the fractional part. For example, 0.5 represents one-half (1/2), and 0.75 represents three-quarters (3/4).
-
Percentages: Percentages represent a fraction or decimal as parts per hundred. The symbol "%" is used to denote a percentage. For example, 50% means 50 parts out of 100, which is equivalent to 0.5 or 1/2.
Converting 4/7 to a Percentage: Step-by-Step Guide
The process of converting a fraction to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case:
4 ÷ 7 ≈ 0.57142857
The result is an approximate decimal because the division results in a repeating decimal (0.571428571428...). We can round this to a certain number of decimal places depending on the required level of accuracy. For our purposes, we'll use four decimal places: 0.5714.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. Therefore:
0.5714 x 100 = 57.14%
Therefore, 4/7 is approximately 57.14%.
Understanding the Significance of Approximation
It's crucial to understand that the conversion of 4/7 to a percentage results in an approximation. The decimal representation of 4/7 is a repeating decimal, meaning the digits after the decimal point repeat infinitely. Rounding is necessary to represent it in a practical way. The level of accuracy required dictates how many decimal places we should round to. For most everyday purposes, rounding to two decimal places (57.14%) is sufficient. However, in situations requiring higher precision, such as scientific calculations or financial modeling, more decimal places might be necessary.
Alternative Methods for Conversion
While the method above is the most straightforward, other approaches exist to convert fractions to percentages. Let's explore one alternative:
Method using equivalent fractions:
The goal is to find an equivalent fraction where the denominator is 100. However, this is not always possible, especially with fractions like 4/7 that don't have a direct relationship with 100. In such cases, the first method (decimal conversion) remains the most practical.
Real-World Applications of Percentage Conversions
Understanding percentage calculations is essential in numerous real-world situations:
-
Financial Calculations: Calculating interest rates, discounts, taxes, and profit margins all involve percentage conversions.
-
Data Analysis: Percentages are used extensively to represent proportions and trends in data analysis, such as in market research, scientific studies, and economic indicators.
-
Everyday Life: Understanding percentages helps us make informed decisions about everyday purchases, comparing prices, and evaluating deals.
Frequently Asked Questions (FAQ)
Q1: Why is the decimal representation of 4/7 a repeating decimal?
A1: The decimal representation of a fraction is a repeating decimal when the denominator of the fraction, in its simplest form, contains prime factors other than 2 and 5. Since 7 is a prime number other than 2 or 5, the decimal representation of 4/7 will be a repeating decimal.
Q2: How can I improve the accuracy of my percentage conversion?
A2: You can improve accuracy by using more decimal places in your calculation. For example, instead of rounding to two decimal places, you could round to four or even more, depending on the required level of precision. Using a calculator with higher precision is also advisable.
Q3: Can all fractions be accurately converted to percentages?
A3: Fractions with denominators that only have 2 and/or 5 as prime factors will have terminating decimal representations and can be converted to exact percentages. Fractions with other prime factors in their denominators will result in repeating decimals, requiring approximation when converting to a percentage.
Q4: What are some common mistakes to avoid when converting fractions to percentages?
A4: Common mistakes include: * Incorrectly dividing the numerator by the denominator. * Forgetting to multiply the decimal by 100. * Incorrectly rounding the decimal to the required number of decimal places.
Conclusion
Converting 4/7 to a percentage is a fundamental mathematical operation with far-reaching applications. While the result (approximately 57.14%) is easily obtained through a simple division and multiplication, a deeper understanding of the underlying principles of fractions, decimals, and percentages provides a more robust grasp of the concept. Remembering to account for the possibility of repeating decimals and understanding the need for approximation are key elements in mastering this crucial skill. The ability to accurately and confidently perform these conversions is vital for success in various academic and professional pursuits. By practicing the steps outlined and understanding the nuances discussed, you'll become proficient in this essential mathematical skill. Remember that accurate calculation, attention to detail, and understanding the context of your application are paramount.
Latest Posts
Latest Posts
-
12 Weeks From Todays Date
Sep 21, 2025
-
36 5 Degrees Celsius To Fahrenheit
Sep 21, 2025
-
How Big Is Vancouver Island
Sep 21, 2025
-
Largest Warehouse In The World
Sep 21, 2025
-
Railway Stations On Monopoly Board
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4 7 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.