4 7 As A Percent
sportsmenna
Sep 23, 2025 · 5 min read
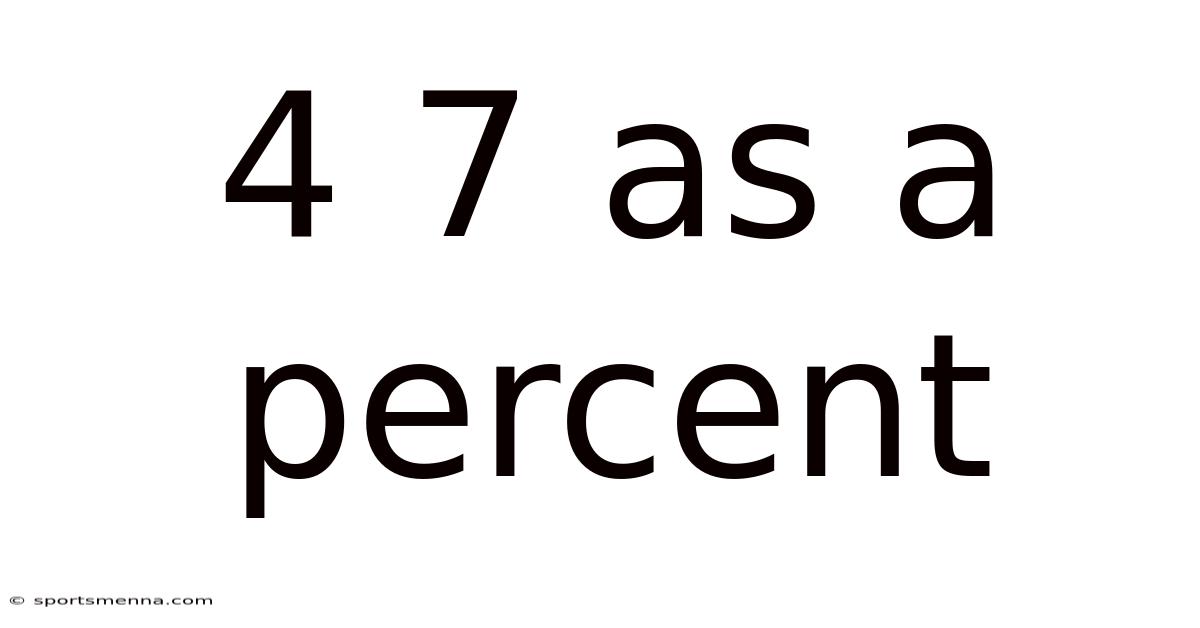
Table of Contents
Decoding 4/7 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to analyzing data and understanding financial reports. This article will delve deep into the process of converting the fraction 4/7 into a percentage, exploring different methods, explaining the underlying concepts, and providing a comprehensive understanding of the topic. We'll also address common questions and misconceptions surrounding percentage calculations.
Introduction: Understanding Fractions and Percentages
Before we dive into converting 4/7 to a percentage, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 4/7, 4 is the numerator and 7 is the denominator. This means we're considering 4 parts out of a total of 7 equal parts.
A percentage, on the other hand, represents a fraction out of 100. The term "percent" literally means "per hundred." So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Converting fractions to percentages involves finding the equivalent fraction with a denominator of 100, or using a more general method involving division.
Method 1: Converting 4/7 to a Percentage using Division
The most straightforward method to convert 4/7 to a percentage involves dividing the numerator (4) by the denominator (7) and then multiplying the result by 100. This process effectively scales the fraction to represent parts per hundred.
-
Divide the numerator by the denominator: 4 ÷ 7 ≈ 0.5714
-
Multiply the result by 100: 0.5714 × 100 ≈ 57.14
Therefore, 4/7 is approximately equal to 57.14%. Note that we use the "approximately equal to" symbol (≈) because the division results in a repeating decimal, which we've rounded to two decimal places for practical purposes. In many contexts, rounding to two decimal places provides sufficient accuracy for percentage calculations.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
While the division method is generally faster and easier, understanding the concept of equivalent fractions is crucial for a deeper grasp of percentage conversions. This method involves finding a fraction equivalent to 4/7 that has a denominator of 100.
Unfortunately, there's no whole number we can multiply 7 by to get exactly 100. This means we can't find a perfectly equivalent fraction with a denominator of 100. However, we can find an approximation.
To achieve this approximation, we can set up a proportion:
4/7 = x/100
To solve for x, we cross-multiply:
7x = 400
x = 400/7 ≈ 57.14
This again gives us approximately 57.14%. This method highlights the principle behind percentage conversions: finding how many parts out of 100 are equivalent to the original fraction.
Method 3: Using a Calculator
Modern calculators make the conversion process incredibly simple. Most calculators have a percentage function (%) or can directly handle fraction-to-decimal conversions. Simply input 4/7 and then multiply by 100 to obtain the percentage.
Understanding the Decimal Representation: Recurring Decimals
As we've seen, the decimal representation of 4/7 (0.571428571428...) is a recurring decimal. This means the sequence of digits (571428) repeats infinitely. When converting to a percentage, we need to round the decimal to a suitable number of decimal places depending on the required level of precision. For most everyday applications, rounding to two decimal places (57.14%) is perfectly adequate.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is vital in various real-world situations. Here are a few examples:
-
Sales and Discounts: If a store offers a 4/7 discount on an item, understanding that this is approximately a 57.14% discount is crucial for calculating the final price.
-
Financial Analysis: In finance, percentages are widely used to represent returns on investment, interest rates, and various financial ratios. Understanding fraction-to-percentage conversion is essential for interpreting financial data.
-
Data Analysis and Statistics: Percentages are frequently employed to represent proportions and probabilities in statistical analysis. Converting fractions to percentages simplifies the interpretation of results and facilitates comparisons.
-
Everyday Calculations: From calculating tips in restaurants to understanding survey results, percentage calculations are commonplace in daily life.
Frequently Asked Questions (FAQ)
-
Q: Is 57.14% the exact percentage equivalent of 4/7?
- A: No, 57.14% is an approximation. The decimal representation of 4/7 is a recurring decimal, meaning the digits repeat infinitely. 57.14% is a rounded approximation accurate to two decimal places.
-
Q: Why do we multiply by 100 when converting a fraction to a percentage?
- A: A percentage represents parts per hundred. Multiplying by 100 scales the fraction to express it in terms of "parts per hundred," which is the definition of a percentage.
-
Q: What if I need more precision than two decimal places?
- A: If higher precision is needed, you can simply round the decimal representation of 4/7 to more decimal places. For instance, you could use 57.1429% or even more decimal places depending on the context.
-
Q: Can I convert other fractions to percentages using the same method?
- A: Yes, absolutely. The methods described in this article—division, equivalent fractions, or using a calculator—can be applied to convert any fraction to its percentage equivalent.
Conclusion: Mastering Percentage Conversions
Converting fractions like 4/7 to percentages is a fundamental mathematical skill with far-reaching practical applications. Understanding the underlying principles, whether through direct division, finding equivalent fractions, or utilizing a calculator, empowers you to confidently navigate numerous real-world scenarios involving percentages. Remember to choose the level of precision appropriate for the given context, understanding that recurring decimals often necessitate rounding to achieve a manageable and meaningful percentage representation. By mastering this skill, you enhance your ability to interpret data, make informed decisions, and confidently handle various percentage-based calculations in your daily life and professional endeavors.
Latest Posts
Latest Posts
-
Presents That Begin With J
Sep 23, 2025
-
Romeo And Juliet Actual Story
Sep 23, 2025
-
Smallest River In The World
Sep 23, 2025
-
75 Degrees Celsius To Fahrenheit
Sep 23, 2025
-
Can Rowan Berries Kill You
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.