3 Divided By 1 5
sportsmenna
Sep 23, 2025 · 6 min read
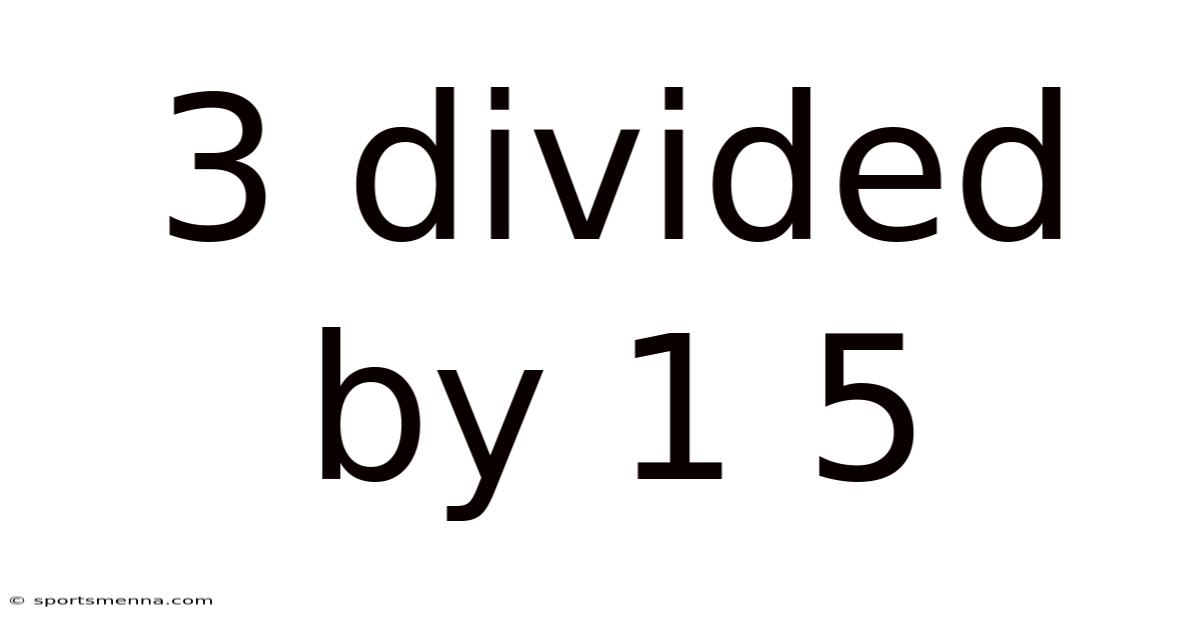
Table of Contents
Understanding 3 Divided by 1.5: A Deep Dive into Division
This article explores the seemingly simple calculation of 3 divided by 1.5, delving beyond the immediate answer to illuminate the underlying principles of division, its various interpretations, and its practical applications in everyday life and advanced mathematics. We'll cover different approaches to solving this problem, address common misconceptions, and explore related concepts to build a robust understanding of this fundamental mathematical operation. This guide will be beneficial for students at various levels, from elementary school to those pursuing higher-level mathematics.
Introduction: Why 3 Divided by 1.5 Matters
The division problem 3 ÷ 1.5 might seem trivial at first glance. However, mastering this seemingly simple calculation provides a foundational understanding of division itself. It's a stepping stone to more complex mathematical operations, and understanding the "why" behind the answer is crucial for developing strong mathematical reasoning skills. This seemingly simple division problem allows us to explore multiple methods of calculation, each offering valuable insights into the nature of division. The application of this concept extends far beyond simple arithmetic, touching upon fractions, decimals, and even abstract algebraic concepts.
Method 1: Long Division
The traditional method of long division can be applied to solve 3 ÷ 1.5. However, since 1.5 is a decimal, we'll need to adjust our approach. The key is to remove the decimal point. We can do this by multiplying both the divisor (1.5) and the dividend (3) by 10:
- 1.5 x 10 = 15
- 3 x 10 = 30
Now our problem becomes 30 ÷ 15. Using long division:
2
15 | 30
-30
0
Therefore, 30 ÷ 15 = 2. Since we multiplied both numbers by 10, the answer remains the same: 3 ÷ 1.5 = 2. This method showcases the importance of manipulating numbers to simplify calculations while maintaining mathematical accuracy.
Method 2: Fraction Conversion
We can express the division problem as a fraction: 3/1.5. Dealing with decimals in fractions can be cumbersome, so let's convert 1.5 into a fraction: 1.5 = 3/2. Our problem now transforms into:
3 ÷ (3/2) This is equivalent to 3 x (2/3).
Notice how division by a fraction becomes multiplication by its reciprocal. This is a fundamental concept in arithmetic. Simplifying the expression:
(3 x 2) / 3 = 6/3 = 2
This method effectively demonstrates the relationship between division and fractions, highlighting the importance of understanding reciprocal values.
Method 3: Decimal Division
While long division is effective, we can directly perform decimal division:
2
1.5 | 3.0
-3.0
0.0
This method, although seemingly straightforward, emphasizes the procedure of decimal division, reinforcing the process of aligning decimal points and carrying out the division as with whole numbers. It's a practical approach for quick mental calculation or when a calculator is not readily available.
Method 4: Understanding the Concept of Division
Division can be understood in several ways. In this case, we're asking: "How many times does 1.5 fit into 3?" We can visualize this by imagining three units, and then repeatedly subtracting 1.5 until we reach zero. We'd find we can do this twice: 3 - 1.5 = 1.5, and 1.5 - 1.5 = 0. This visual approach helps solidify the concept of division as repeated subtraction.
Understanding Division in Different Contexts
The concept of division extends far beyond basic arithmetic. Let's explore some broader contexts:
-
Equal Sharing: Imagine sharing 3 pizzas equally among 1.5 people (perhaps a group of one adult and a half-adult). How much pizza does each person get? The answer, 2, can represent 2 whole pizzas per person. This scenario helps illustrate the application of division in real-world situations involving proportional sharing.
-
Rate and Ratio: If a car travels 3 kilometers in 1.5 hours, what's its speed? Dividing the distance by the time gives us a speed of 2 kilometers per hour. Here, division is used to find a rate (speed) by comparing two related quantities.
-
Scaling and Proportion: If a recipe calls for 1.5 cups of flour to make one cake, how many cakes can you make with 3 cups of flour? The answer (2) is obtained through division. This shows how division helps in scaling proportions in various contexts such as cooking or engineering.
-
Abstract Algebra: Division plays a crucial role in abstract algebra, particularly in fields and rings where the properties of division (and its inverse, multiplication) define the structure of the algebraic system. While beyond the scope of this basic example, it's worth noting that this simple operation has profound implications in advanced mathematics.
Addressing Common Misconceptions:
-
Decimal Anxiety: Many students struggle with decimal division. Remember, the key is to understand the underlying principles. Converting to fractions or multiplying to remove the decimal can significantly simplify the process.
-
Confusing Division and Subtraction: Division is repeated subtraction. While related, they're not interchangeable. Division finds how many times a number fits into another, while subtraction simply reduces one number by another.
-
Order of Operations: In complex calculations, remember the order of operations (PEMDAS/BODMAS). Division and multiplication are typically performed from left to right, before addition and subtraction.
Frequently Asked Questions (FAQ):
-
Q: Can I use a calculator to solve 3 ÷ 1.5? A: Absolutely! Calculators are valuable tools, particularly for more complex calculations. However, understanding the underlying principles remains crucial.
-
Q: What if the numbers were different? A: The principles remain the same. Use any of the methods discussed (long division, fraction conversion, decimal division) depending on your preference and the complexity of the numbers involved.
-
Q: What happens if I divide by zero? A: Division by zero is undefined in mathematics. It's a fundamental concept that leads to mathematical inconsistencies. Never attempt to divide by zero.
-
Q: Are there other ways to represent this division problem? A: Yes! You could express it as 3/1.5, 3:1.5 or even using other mathematical notations depending on the context. The core concept remains the same.
Conclusion: The Significance of a Simple Calculation
The seemingly simple calculation of 3 divided by 1.5 provides a rich opportunity to explore the multifaceted nature of division. From long division and fraction manipulation to real-world applications in sharing, rates, and scaling, the concept transcends basic arithmetic to underpin more complex mathematical concepts. Understanding not just the how but also the why behind the answer (2) empowers students with a deeper and more versatile grasp of mathematical principles, laying a solid foundation for future learning and problem-solving. The core message is not just about getting the right answer but about understanding the process, the context, and the power of a fundamental mathematical operation. This understanding is essential for tackling more advanced mathematical challenges and appreciating the interconnectedness of mathematical concepts. The journey from 3 ÷ 1.5 = 2 is not just about reaching the answer; it's about the journey of understanding and applying mathematical principles.
Latest Posts
Latest Posts
-
Gas Is Renewable Or Nonrenewable
Sep 23, 2025
-
John Coleman On Doc Martin
Sep 23, 2025
-
215 Is What Area Code
Sep 23, 2025
-
How Long Is The Pencil
Sep 23, 2025
-
How Do You Evolve Swadloon
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.