3 8 As A Percentage
sportsmenna
Sep 20, 2025 · 5 min read
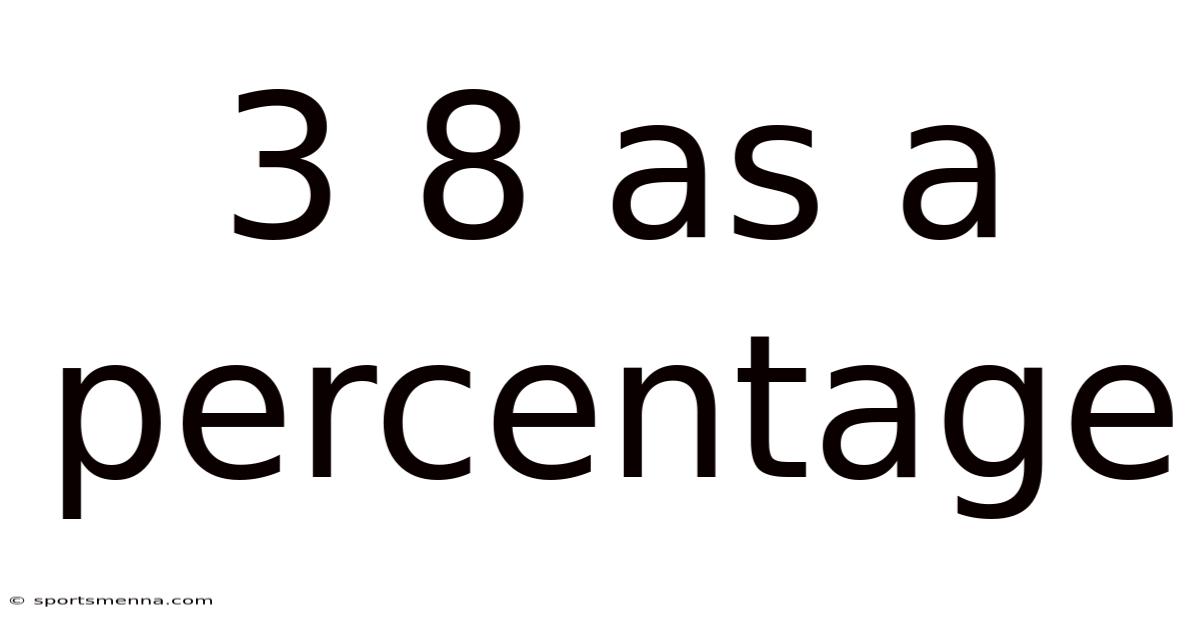
Table of Contents
Decoding 3/8 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning numerous fields, from finance and statistics to everyday calculations. This comprehensive guide delves into the conversion of the fraction 3/8 into a percentage, explaining the process step-by-step and exploring related concepts to solidify your understanding. We'll cover the method, explore the practical implications, and address frequently asked questions, ensuring you gain a complete grasp of this important concept.
Understanding Fractions and Percentages
Before diving into the specific conversion of 3/8, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (per centum in Latin). Percentages are widely used to represent proportions, rates, and changes. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 3/8 to a Percentage: The Step-by-Step Process
Converting a fraction to a percentage involves two main steps:
-
Converting the fraction to a decimal: To do this, we divide the numerator (3) by the denominator (8). 3 ÷ 8 = 0.375
-
Converting the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. 0.375 x 100 = 37.5%
Therefore, 3/8 is equal to 37.5%.
A Deeper Dive into the Conversion Process: Mathematical Rationale
The conversion process relies on the fundamental relationship between fractions, decimals, and percentages. Let's explore this relationship more deeply:
-
Fractions as Division: A fraction essentially represents a division problem. The numerator is divided by the denominator. This division results in a decimal value.
-
Decimals and Place Value: The decimal system uses powers of 10 (10, 100, 1000, etc.) to represent values less than one. Each place to the right of the decimal point represents a decreasing power of 10.
-
Percentage as a Fraction of 100: A percentage is simply a fraction where the denominator is always 100. Multiplying a decimal by 100 effectively shifts the decimal point two places to the right, converting it into a fraction with a denominator of 100 (which is the definition of a percentage).
In the case of 3/8, the division (3 ÷ 8 = 0.375) gives us the decimal representation. Multiplying by 100 (0.375 x 100 = 37.5) then expresses this decimal as a fraction with 100 as the denominator, resulting in 37.5%.
Practical Applications of 3/8 and 37.5%
Understanding the equivalence between 3/8 and 37.5% has numerous practical applications. Here are a few examples:
-
Calculating Discounts: If a store offers a 37.5% discount on an item, you can use this knowledge to quickly calculate the discount amount.
-
Analyzing Data: In statistics, percentages are commonly used to represent proportions within a dataset. Understanding 3/8 as 37.5% allows for easy interpretation of data.
-
Portioning Ingredients: In cooking, recipes often require fractions of ingredients. Knowing that 3/8 is equal to 37.5% can assist in accurately measuring ingredients if you prefer using percentage-based measurements.
-
Financial Calculations: Interest rates, profit margins, and other financial calculations often involve percentages. Understanding the relationship between fractions and percentages is crucial for accurate financial computations.
-
Everyday Life: Many situations in everyday life require the understanding of proportions and percentages, from splitting bills equally to understanding sales tax.
Alternative Methods for Conversion: Using Proportions
While the direct division method is straightforward, we can also employ proportions to convert 3/8 to a percentage. We can set up a proportion:
3/8 = x/100
To solve for x (the percentage), we cross-multiply:
8x = 300
x = 300/8
x = 37.5
This confirms that 3/8 is equivalent to 37.5%. This method highlights the inherent relationship between fractions and percentages as proportional representations.
Expanding the Understanding: Working with Other Fractions
The same principles used to convert 3/8 to a percentage can be applied to any fraction. To convert any fraction (a/b) to a percentage:
- Divide the numerator (a) by the denominator (b).
- Multiply the resulting decimal by 100 and add the "%" symbol.
For example, to convert 1/4 to a percentage:
- 1 ÷ 4 = 0.25
- 0.25 x 100 = 25%
Frequently Asked Questions (FAQ)
Q1: Is there a way to quickly estimate the percentage equivalent of a fraction without a calculator?
A1: Yes, for some common fractions, mental estimation is possible. For example, you might remember that 1/4 = 25%, 1/2 = 50%, and 3/4 = 75%. For other fractions, understanding that 1/10 = 10% can be a helpful starting point for estimations.
Q2: Why is it important to understand the relationship between fractions and percentages?
A2: Understanding this relationship is crucial for various mathematical and real-world applications. It allows for easier comparison of different proportions, interpretation of data, and accurate calculations in diverse fields.
Q3: Can a percentage be greater than 100%?
A3: Yes, a percentage can be greater than 100%. This indicates that the part is larger than the whole, which is often used in contexts where growth or increase is being described (e.g., a 110% increase in sales).
Q4: Are there any online tools or calculators that can help with fraction-to-percentage conversions?
A4: Many online calculators are available to perform these conversions quickly and efficiently. However, understanding the underlying process is crucial for building a strong mathematical foundation.
Conclusion: Mastering the Conversion
Converting 3/8 to a percentage (37.5%) is a straightforward process involving dividing the numerator by the denominator and multiplying the resulting decimal by 100. This fundamental skill empowers you to handle various mathematical problems and real-world scenarios involving proportions and percentages. By understanding the underlying mathematical principles and employing different conversion methods, you can confidently navigate the world of fractions and percentages with increased proficiency. Remember, practice is key to mastering this valuable skill!
Latest Posts
Latest Posts
-
What Is Brown In French
Sep 20, 2025
-
Nearest Airport To Lourdes France
Sep 20, 2025
-
5 9 As A Percentage
Sep 20, 2025
-
Reciprocal Of 2 1 2
Sep 20, 2025
-
73 4kg In Stone And Lbs
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 8 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.