3 3 3 X 3
sportsmenna
Sep 21, 2025 · 6 min read
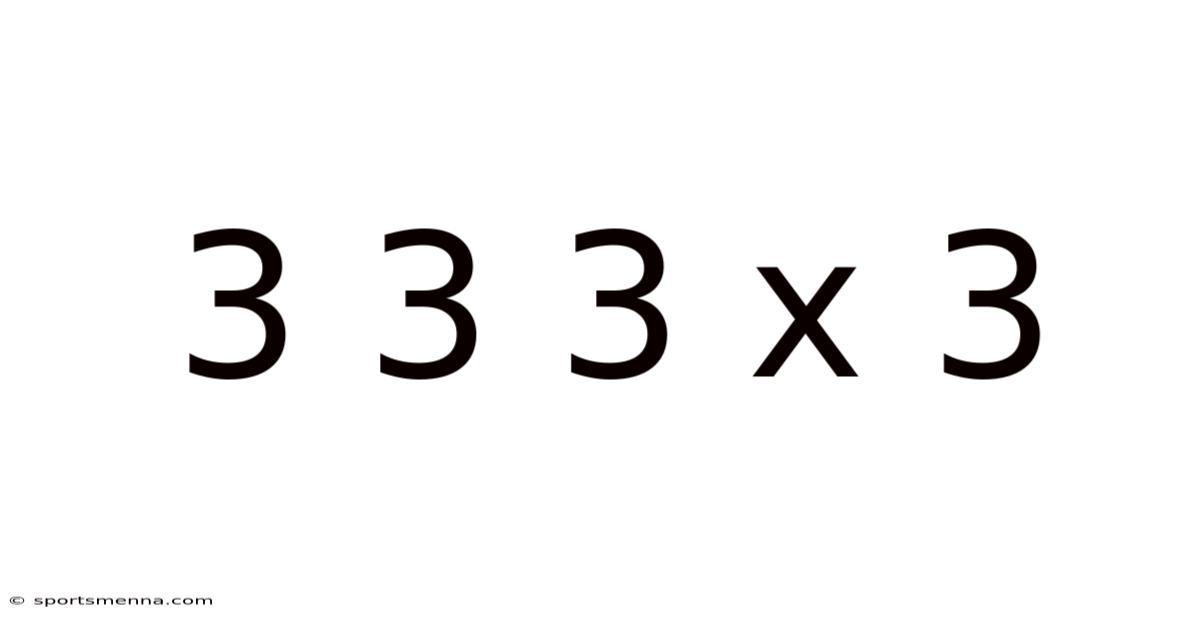
Table of Contents
Decoding the Mystery: Exploring the Mathematical and Philosophical Implications of 3 x 3 x 3 x 3
The seemingly simple mathematical expression "3 x 3 x 3 x 3" – or 3⁴ – holds a surprising depth, inviting exploration beyond basic arithmetic. This article delves into the multifaceted nature of this expression, examining its mathematical properties, its connections to various fields like geometry and computer science, and even venturing into the realm of philosophical interpretations. Understanding this seemingly simple equation opens doors to a richer appreciation of numbers and their profound implications.
I. The Fundamental Calculation: 3 to the Power of 4
At its core, 3 x 3 x 3 x 3 is a calculation of exponentiation. It represents 3 multiplied by itself four times. The straightforward calculation yields the answer 81. This is the bedrock upon which further exploration is built. While simple to compute, the significance of this number extends far beyond its immediate result.
II. Geometric Interpretations: Cubes and Dimensions
The number 81, derived from 3⁴, possesses compelling geometric interpretations. Imagine a cube. A cube has three dimensions: length, width, and height. If each side of the cube has a length of 3 units, then the total number of unit cubes that would fill this larger cube is 3 x 3 x 3 = 27. Taking this a step further, consider a four-dimensional hypercube (a tesseract). While difficult to visualize directly, a hypercube can be conceptually understood as a cube extended into a fourth dimension. If each side of this hypercube has a length of 3 units, then the total number of unit hypercubes within the larger hypercube would be 3 x 3 x 3 x 3 = 81. This elegantly demonstrates how the equation transcends simple arithmetic and connects to higher-dimensional geometries.
III. The Number 81: Properties and Significance
The number 81 itself holds several interesting mathematical properties:
-
Square of a Square: 81 is the square of 9 (9² = 81), and 9 is itself a perfect square (3² = 9). This nested squaring highlights the iterative nature of the original equation and the compounding effect of repeated multiplication.
-
Divisors: The divisors of 81 are 1, 3, 9, 27, and 81. This simple list reveals factors and relationships crucial in number theory.
-
Digital Root: The digital root of 81 (8 + 1 = 9) is a significant number in numerology and various mystical traditions, often associated with completion and spiritual enlightenment. This, of course, is a non-mathematical interpretation, but it demonstrates the reach of the number's symbolism.
-
Decimal Representation: The decimal representation of 81 is straightforward and concise, contrasting with some numbers with more complex representations that lead to deeper mathematical analysis.
IV. Applications in Computer Science and Data Structures
In computer science, the number 81 (and its root, 3) surfaces frequently:
-
3-ary Trees: Data structures such as ternary trees (trees with three children per node) employ base-3 calculations for indexing and navigation. The exponential nature of 3⁴ can influence the complexity and efficiency of algorithms that operate on such trees.
-
3D Graphics and Modeling: In 3D modeling and computer graphics, the concept of cubes and higher-dimensional structures is pivotal. The calculation 3 x 3 x 3 x 3 could represent the number of voxels (volume pixels) in a 3x3x3x3 structure.
-
Hash Tables and Data Organization: Hash functions, used for efficient data retrieval, often involve calculations modulo a prime number. While 81 isn't prime, its factors and their relations to prime numbers can influence the design and performance of such functions.
V. Beyond the Numbers: Philosophical Musings
While the primary focus of this exploration has been the mathematical aspects, the expression 3 x 3 x 3 x 3 lends itself to philosophical reflections:
-
The Power of Iteration: The repeated multiplication (iteration) in 3⁴ illustrates the power of compounding and iterative processes. This is applicable across various domains, from financial growth to biological systems where small changes accumulate over time.
-
The Significance of Structure: The structured nature of the calculation highlights the importance of order and organization in understanding complex systems. The simple act of multiplication becomes a building block for more intricate mathematical and scientific models.
-
Exploring Higher Dimensions: The connection between 3⁴ and the concept of the four-dimensional hypercube expands our understanding of dimensionality and how we conceptualize space and reality. It challenges our intuition and forces us to consider dimensions beyond our immediate perception.
-
The Relationship Between the Simple and the Complex: This simple equation reveals a rich tapestry of connections and applications. It illustrates how even seemingly basic concepts can underlie complex systems and lead to deep understanding.
VI. Frequently Asked Questions (FAQ)
-
Q: Is 81 a prime number? A: No, 81 is not a prime number. A prime number is only divisible by 1 and itself. 81 is divisible by 3, 9, and 27.
-
Q: What are some other ways to represent 3⁴? A: Besides 3 x 3 x 3 x 3, you can represent it as 81, or as powers of other numbers (e.g., 9²).
-
Q: What is the significance of the base number (3) in this equation? A: The base number 3 is crucial as it defines the iterative multiplication process. Changing the base number would dramatically change the result and its geometrical interpretations.
-
Q: Are there real-world applications of this calculation beyond mathematics and computer science? A: While its direct applications may be predominantly in these fields, the underlying principles (exponentiation, iteration, dimensionality) apply to many areas, including physics, engineering, finance, and even social sciences in understanding growth and compounding effects.
-
Q: Can this equation be used in other mathematical fields, such as calculus? A: While the equation itself might not be directly used in calculus, the concepts of exponentiation, functions, and limits are fundamental to calculus and its understanding. The function f(x) = 3ˣ is a classic example of an exponential function studied in calculus.
VII. Conclusion: More Than Just a Calculation
The seemingly straightforward calculation of 3 x 3 x 3 x 3 = 81 reveals layers of depth and complexity extending far beyond its initial simplicity. From its geometric interpretations in higher dimensions to its applications in computer science and its broader philosophical implications, this equation acts as a microcosm of the vastness and interconnectedness within mathematics and beyond. Understanding the intricacies of 3⁴ provides a deeper appreciation for the power of numbers, the elegance of mathematical structures, and the profound connections between seemingly disparate fields of knowledge. It is a testament to how even the most basic mathematical concepts can unlock a wealth of insight and understanding. The exploration of this seemingly simple calculation reveals that the true power often lies not just in the answer, but in the journey of discovery itself.
Latest Posts
Latest Posts
-
What Is Dextrinization In Food
Sep 21, 2025
-
Air As A Raising Agent
Sep 21, 2025
-
What Is Wales In Welsh
Sep 21, 2025
-
85 Degrees F To C
Sep 21, 2025
-
Ammonium Chloride And Sodium Hydroxide
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 3 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.