2 8 As A Percent
sportsmenna
Sep 20, 2025 · 6 min read
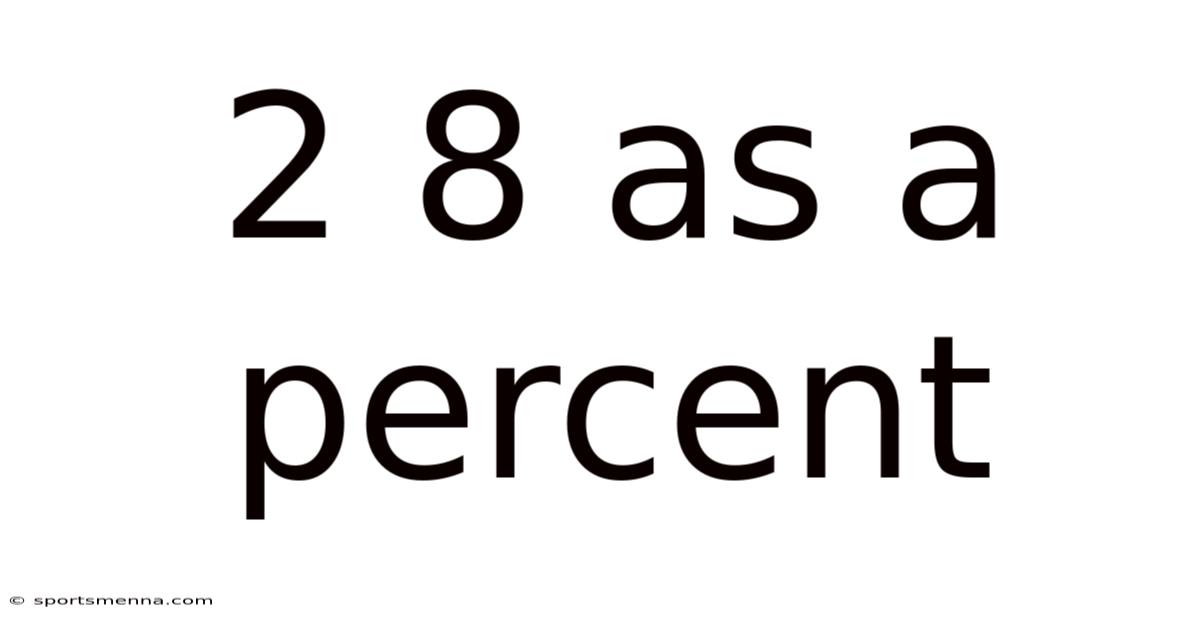
Table of Contents
Understanding 2/8 as a Percent: A Comprehensive Guide
What does 2/8 as a percent actually mean? This seemingly simple fraction holds the key to understanding fundamental concepts in mathematics, particularly the conversion between fractions, decimals, and percentages. This comprehensive guide will not only show you how to calculate 2/8 as a percentage but will also delve deeper into the underlying principles, providing you with a solid foundation for tackling similar problems in the future. We'll explore different methods of calculation, address common misconceptions, and even touch upon the practical applications of percentage calculations in everyday life.
Understanding Fractions, Decimals, and Percentages
Before we dive into converting 2/8 to a percentage, let's briefly review the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts in the whole.
-
Decimals: Represent a part of a whole using a base-ten system. The position of each digit after the decimal point represents a power of ten (tenths, hundredths, thousandths, etc.).
-
Percentages: Represent a part of a whole as a proportion of 100. The symbol "%" signifies "per hundred."
These three representations are interconnected and can be easily converted from one to another. Understanding these interconnections is crucial for mastering percentage calculations.
Method 1: Simplifying the Fraction
The first and often the easiest method to convert 2/8 to a percentage is to simplify the fraction before converting it to a decimal and then a percentage.
Step 1: Simplify the Fraction
The fraction 2/8 can be simplified by finding the greatest common divisor (GCD) of the numerator (2) and the denominator (8). The GCD of 2 and 8 is 2. Dividing both the numerator and the denominator by 2, we get:
2 ÷ 2 / 8 ÷ 2 = 1/4
This simplified fraction, 1/4, represents the same proportion as 2/8.
Step 2: Convert the Fraction to a Decimal
To convert the simplified fraction 1/4 to a decimal, we divide the numerator (1) by the denominator (4):
1 ÷ 4 = 0.25
Step 3: Convert the Decimal to a Percentage
To convert the decimal 0.25 to a percentage, we multiply it by 100 and add the percentage symbol (%):
0.25 × 100 = 25%
Therefore, 2/8 is equal to 25%.
Method 2: Direct Conversion to a Decimal
Alternatively, we can directly convert 2/8 to a decimal and then to a percentage without simplifying the fraction first.
Step 1: Convert the Fraction to a Decimal
Divide the numerator (2) by the denominator (8):
2 ÷ 8 = 0.25
Step 2: Convert the Decimal to a Percentage
Multiply the decimal 0.25 by 100 and add the percentage symbol (%):
0.25 × 100 = 25%
This method yields the same result: 2/8 is equal to 25%.
Method 3: Using Proportions
This method provides a deeper understanding of the underlying mathematical principle. We can set up a proportion to solve for the percentage.
We know that a percentage is a fraction out of 100. So we can set up the following proportion:
2/8 = x/100
Where 'x' represents the percentage we want to find.
To solve for 'x', we can cross-multiply:
8x = 200
Now, divide both sides by 8:
x = 200 ÷ 8 = 25
Therefore, x = 25, meaning 2/8 is equal to 25%.
Understanding the Concept of Percentage in Real-World Scenarios
The ability to convert fractions to percentages is not merely an academic exercise; it's a crucial skill with numerous real-world applications. Consider these examples:
-
Discounts: If a store offers a 25% discount on an item, understanding that this is equivalent to 1/4 helps calculate the savings easily.
-
Sales Tax: Calculating sales tax involves converting a percentage (e.g., 6%) to a decimal to determine the amount of tax to be added to the price of a good or service.
-
Interest Rates: Understanding interest rates, whether on loans or savings accounts, requires a solid grasp of percentage calculations.
-
Statistical Data: Percentages are frequently used to represent data in various fields, including finance, science, and social studies. Understanding how to interpret and calculate percentages is vital for analyzing and understanding this data.
-
Surveys and Polls: Results of surveys and polls are often presented as percentages, representing the proportion of respondents who chose a specific answer.
Addressing Common Misconceptions
A common mistake is to confuse the numerator and denominator when converting fractions to percentages. Always remember that the numerator represents the part and the denominator represents the whole.
Another common error is incorrectly multiplying or dividing by 10 or 1000 instead of 100 when converting between decimals and percentages. Remember, to convert a decimal to a percentage, you multiply by 100; to convert a percentage to a decimal, you divide by 100.
Frequently Asked Questions (FAQs)
Q: Can I convert any fraction to a percentage?
A: Yes, absolutely. Any fraction can be converted to a percentage by first converting it to a decimal and then multiplying by 100.
Q: What if the fraction results in a repeating decimal?
A: If the fraction results in a repeating decimal, you can round the decimal to a certain number of decimal places before converting it to a percentage. The level of precision depends on the context of the problem.
Q: Is there a way to calculate percentages without a calculator?
A: Yes, you can use mental math techniques or manual calculations for simpler fractions. For instance, knowing that 1/4 = 25%, 1/2 = 50%, and 1/10 = 10% can help in approximating percentages.
Q: Why is understanding percentages important?
A: Understanding percentages is crucial for making informed decisions in various aspects of life, from personal finance to professional fields. It allows you to analyze data, compare values, and understand proportions accurately.
Conclusion
Converting 2/8 to a percentage is a fundamental concept in mathematics with wide-ranging applications. By understanding the underlying principles of fractions, decimals, and percentages, you can confidently tackle similar problems and apply this knowledge to real-world situations. Whether you use simplification, direct decimal conversion, or proportions, the final answer remains consistent: 2/8 is equal to 25%. Mastering this skill will undoubtedly enhance your mathematical abilities and equip you with valuable problem-solving skills applicable across various domains. Remember to practice regularly to solidify your understanding and build confidence in tackling percentage calculations.
Latest Posts
Latest Posts
-
Calcium Carbonate And Sulphuric Acid
Sep 20, 2025
-
Comme Si Comme Sa Meaning
Sep 20, 2025
-
What Year Was The Song
Sep 20, 2025
-
Do Women Like Sucking Cock
Sep 20, 2025
-
What Metals Are Not Magnetic
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 2 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.