2 1/2 In Decimal Form
sportsmenna
Sep 23, 2025 · 6 min read
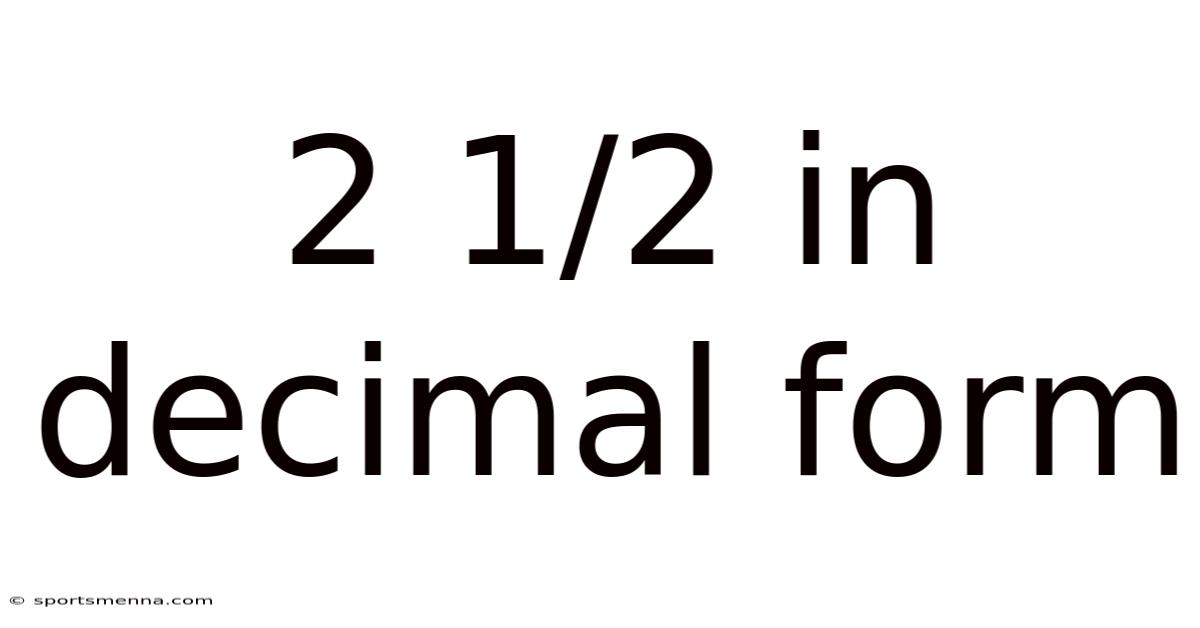
Table of Contents
2 1/2 in Decimal Form: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This article provides a comprehensive guide on converting the mixed number 2 1/2 into its decimal equivalent, explaining the process in detail and exploring related concepts. We'll delve into various methods, discuss the importance of decimal representation, and answer frequently asked questions to solidify your understanding. This guide is perfect for students, educators, and anyone looking to brush up on their fraction-to-decimal conversion skills.
Introduction: Understanding Fractions and Decimals
Before diving into the conversion of 2 1/2, let's briefly review the basics of fractions and decimals. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 1/2, 1 is the numerator and 2 is the denominator. This indicates one out of two equal parts.
A decimal, on the other hand, represents a number using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, 0.5 represents five-tenths, or 5/10.
Converting between fractions and decimals is crucial for various mathematical operations and real-world applications. Understanding this conversion allows for easier calculations, comparisons, and data representation.
Method 1: Converting the Fraction to a Decimal Directly
The simplest method to convert 2 1/2 to decimal form involves understanding the fraction component. The fraction 1/2 represents half, or 0.5. Therefore, 2 1/2 is simply 2 + 0.5 = 2.5.
This method highlights the inherent connection between fractions and decimals. The fraction 1/2 is directly equivalent to the decimal 0.5. This understanding forms the foundation for more complex fraction-to-decimal conversions.
Method 2: Long Division
While the previous method was straightforward for this specific fraction, the long division method provides a more general approach applicable to any fraction. This method is particularly useful for fractions that aren't easily recognizable as simple decimal equivalents.
To use long division, we first convert the mixed number 2 1/2 into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator. To do this, we multiply the whole number (2) by the denominator (2) and add the numerator (1): (2 * 2) + 1 = 5. This gives us the improper fraction 5/2.
Now, we perform long division:
2.5
2 | 5.0
-4
10
-10
0
Dividing 5 by 2, we get 2 with a remainder of 1. Adding a decimal point and a zero to the dividend (5.0), we continue the division. 2 goes into 10 five times, resulting in a final answer of 2.5.
Method 3: Using a Calculator
Modern calculators offer a convenient way to convert fractions to decimals. Simply enter the fraction 2 1/2 (or its improper fraction equivalent, 5/2) into the calculator and press the equals button. The calculator will automatically perform the conversion and display the decimal equivalent: 2.5. While this method is quick and efficient, understanding the underlying mathematical principles remains crucial for developing strong mathematical reasoning skills.
The Significance of Decimal Representation
Representing 2 1/2 as 2.5 offers several advantages:
- Easier Calculations: Decimal numbers are generally easier to use in calculations, especially when dealing with addition, subtraction, multiplication, and division involving other decimal numbers.
- Precise Comparisons: Comparing decimal numbers is simpler than comparing fractions, especially when the fractions have different denominators.
- Data Representation: Many scientific, engineering, and financial applications rely on decimal representation for precise data representation and analysis.
- Universal Understanding: Decimals are universally understood, making communication of numerical data more efficient and less prone to misinterpretation.
Expanding on the Concept: Converting Other Fractions to Decimals
The techniques used to convert 2 1/2 to its decimal form can be extended to other fractions. Here's a breakdown of the process with examples:
- Proper Fractions: Fractions where the numerator is smaller than the denominator (e.g., 3/4). Convert these to decimals using long division or a calculator. 3/4 = 0.75
- Improper Fractions: Fractions where the numerator is larger than or equal to the denominator (e.g., 7/3). Convert these to decimals using long division or a calculator. 7/3 = 2.333... (a repeating decimal)
- Mixed Numbers: Numbers with a whole number part and a fractional part (e.g., 1 2/5). Convert the fractional part to a decimal and add it to the whole number. 1 2/5 = 1 + 0.4 = 1.4
Remember that some fractions result in repeating decimals (e.g., 1/3 = 0.333...), while others result in terminating decimals (e.g., 1/4 = 0.25).
Frequently Asked Questions (FAQ)
Q1: Why is understanding decimal conversion important?
A1: Decimal conversion is crucial for various applications, including simplifying calculations, making precise comparisons, and accurately representing data in various fields like science, engineering, and finance. It also improves your overall mathematical proficiency and problem-solving abilities.
Q2: Can all fractions be converted into terminating decimals?
A2: No, not all fractions can be converted into terminating decimals. Fractions whose denominators have prime factors other than 2 and 5 will result in repeating decimals.
Q3: What if I have a complex fraction?
A3: Complex fractions can be simplified first before converting them to decimals. Simplify the numerator and denominator separately and then perform the division.
Q4: How do I round a repeating decimal?
A4: Repeating decimals can be rounded to a specific number of decimal places based on the required precision. Commonly used rounding rules involve rounding up if the next digit is 5 or greater, and rounding down otherwise.
Q5: Are there any online tools for fraction-to-decimal conversion?
A5: Yes, numerous online calculators and converters are readily available to assist with fraction-to-decimal conversions. However, understanding the underlying mathematical principles remains crucial for building a strong mathematical foundation.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 2 1/2 to its decimal equivalent, 2.5, is a simple yet illustrative example of a fundamental mathematical concept. We've explored several methods, from direct conversion to long division, emphasizing the importance of understanding both fractions and decimals. Mastering this conversion skill is not merely about getting the right answer; it's about gaining a deeper understanding of the relationship between these two fundamental numerical representations. This understanding will serve as a strong foundation for more advanced mathematical concepts and problem-solving. Remember to practice regularly to build confidence and fluency in converting fractions to decimals and vice versa. This skill is invaluable for various aspects of life, from everyday calculations to more complex academic and professional pursuits.
Latest Posts
Latest Posts
-
65 Degree Fahrenheit To Celsius
Sep 23, 2025
-
Gas Is Renewable Or Nonrenewable
Sep 23, 2025
-
John Coleman On Doc Martin
Sep 23, 2025
-
215 Is What Area Code
Sep 23, 2025
-
How Long Is The Pencil
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 1/2 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.