14 20 As A Decimal
sportsmenna
Sep 23, 2025 · 5 min read
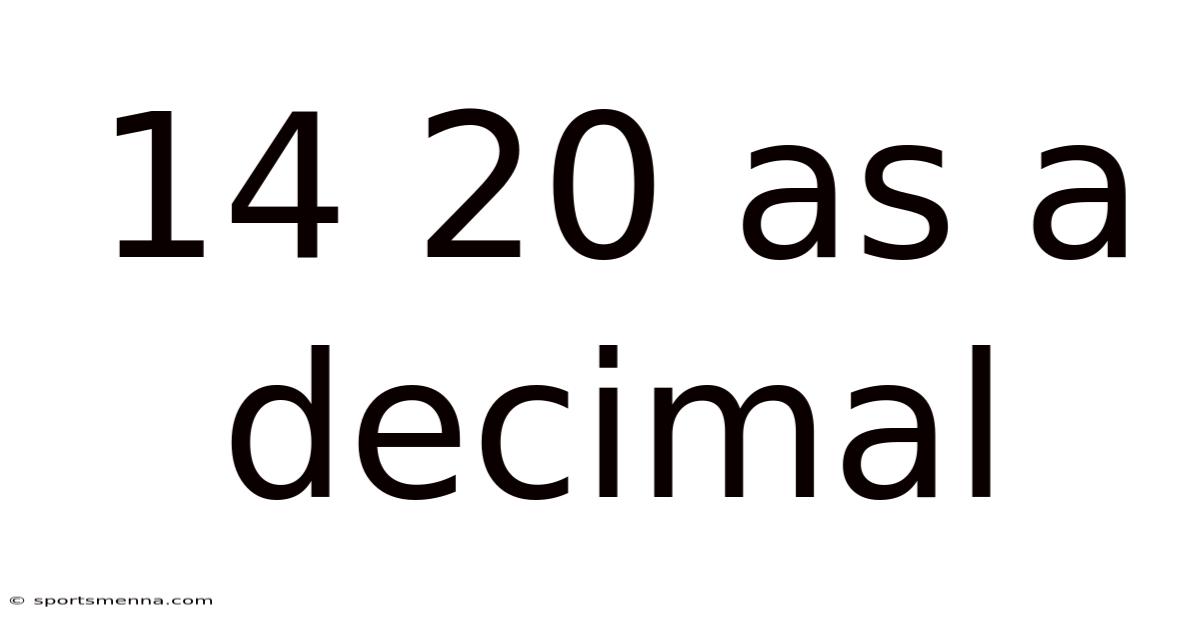
Table of Contents
Decoding 14/20 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article delves deep into the conversion of the fraction 14/20 into its decimal form, explaining the process in detail, exploring related concepts, and addressing frequently asked questions. By the end, you'll not only know the decimal equivalent of 14/20 but also possess a solid understanding of fraction-to-decimal conversions. This comprehensive guide is perfect for students, educators, and anyone looking to strengthen their math skills.
Understanding Fractions and Decimals
Before we dive into the conversion of 14/20, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, is a way of representing a number using base-10, where each digit represents a power of 10. The decimal point separates the whole number part from the fractional part. For example, in the decimal 3.14, '3' represents the whole number, while '.14' represents the fractional part (14 hundredths).
Converting fractions to decimals involves finding the equivalent decimal representation of the fraction. This is typically achieved through division.
Converting 14/20 to a Decimal: The Process
The simplest way to convert 14/20 to a decimal is through division. We divide the numerator (14) by the denominator (20):
14 ÷ 20 = 0.7
Therefore, the decimal equivalent of 14/20 is 0.7.
Simplifying Fractions Before Conversion
While the direct division method works perfectly, simplifying the fraction before conversion can often make the process easier. Simplifying a fraction involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 14 and 20 is 2.
Dividing both the numerator and denominator by 2, we get:
14 ÷ 2 = 7 20 ÷ 2 = 10
This simplifies the fraction to 7/10. Now, converting 7/10 to a decimal is even simpler:
7 ÷ 10 = 0.7
As you can see, we arrive at the same decimal value, 0.7. Simplifying the fraction beforehand can be beneficial, especially when dealing with larger numbers or fractions that are not easily divisible.
Understanding the Decimal Value: 0.7
The decimal 0.7 represents seven tenths. This means it's equivalent to 7 parts out of 10 equal parts of a whole. We can visualize this easily. Imagine a bar divided into 10 equal sections. Shading 7 of those sections would visually represent 0.7 or 7/10.
Alternative Methods for Conversion
While division is the most straightforward method, other techniques can be employed to convert fractions to decimals. These are particularly useful when dealing with fractions with denominators that are powers of 10 (10, 100, 1000, etc.).
-
Equivalent Fractions with a Denominator of a Power of 10: As shown above, converting 14/20 to 7/10 involved finding an equivalent fraction with a denominator of 10. This method is highly efficient for fractions with denominators that are easily converted to powers of 10.
-
Using a Calculator: Calculators can quickly compute the decimal equivalent of any fraction. Simply enter the numerator, followed by the division symbol, and then the denominator.
Percentage Equivalents
Converting a fraction to a decimal also allows for easy conversion to a percentage. To convert a decimal to a percentage, we multiply by 100 and add a percentage sign (%).
0.7 x 100 = 70%
Therefore, 14/20 is equivalent to 70%. This demonstrates the interconnectedness of fractions, decimals, and percentages – all different ways of expressing the same proportion.
Applications of Fraction-to-Decimal Conversion
The ability to convert fractions to decimals is crucial in numerous fields:
-
Finance: Calculating interest rates, discounts, and profit margins often involves working with fractions and decimals.
-
Science: Many scientific measurements and calculations rely on decimal representations of fractions.
-
Engineering: Precise measurements and calculations in engineering projects necessitate the conversion of fractions to decimals for accurate results.
-
Everyday Life: From cooking (measuring ingredients) to splitting bills, understanding fractions and decimals simplifies many everyday tasks.
Expanding Understanding: Different Types of Decimals
The decimal 0.7 is a terminating decimal, meaning it has a finite number of digits after the decimal point. However, not all fractions result in terminating decimals. Some fractions produce repeating decimals, where a sequence of digits repeats infinitely. For example, 1/3 = 0.3333... (the 3 repeats infinitely). Understanding the difference between terminating and repeating decimals is essential for a complete grasp of decimal representation.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a decimal?
A1: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator. The result will either be a terminating decimal or a repeating decimal.
Q2: Is there a limit to the number of decimal places I can use?
A2: While terminating decimals have a finite number of digits, repeating decimals can continue infinitely. In practice, we often round repeating decimals to a specific number of decimal places depending on the level of accuracy required.
Q3: Why is it important to simplify fractions before conversion?
A3: Simplifying fractions reduces the numbers involved, making the division process easier and potentially reducing the chance of calculation errors. It also improves the clarity and understanding of the fraction's value.
Q4: What if the fraction has a negative sign?
A4: If the fraction is negative (e.g., -14/20), the resulting decimal will also be negative (-0.7). The conversion process remains the same, just remember to include the negative sign in the final answer.
Q5: How can I improve my skills in converting fractions to decimals?
A5: Practice is key! Work through various examples, starting with simple fractions and gradually progressing to more complex ones. Use online resources, practice problems, and seek help from teachers or tutors if needed.
Conclusion
Converting 14/20 to a decimal is a straightforward process involving division. Understanding the underlying principles of fractions, decimals, and the different types of decimals (terminating and repeating) strengthens your mathematical foundation. The ability to confidently perform this conversion is invaluable in various academic and real-world applications. Remember to utilize simplification techniques when possible to streamline the process and enhance understanding. By mastering fraction-to-decimal conversions, you build a stronger base for more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
Chocolate Bar Beginning With J
Sep 23, 2025
-
Dialling Code Republic Of Ireland
Sep 23, 2025
-
How Many J In Kj
Sep 23, 2025
-
What Is A Field Database
Sep 23, 2025
-
16 Degrees F To C
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 14 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.