12 15 In Simplest Form
sportsmenna
Sep 21, 2025 · 6 min read
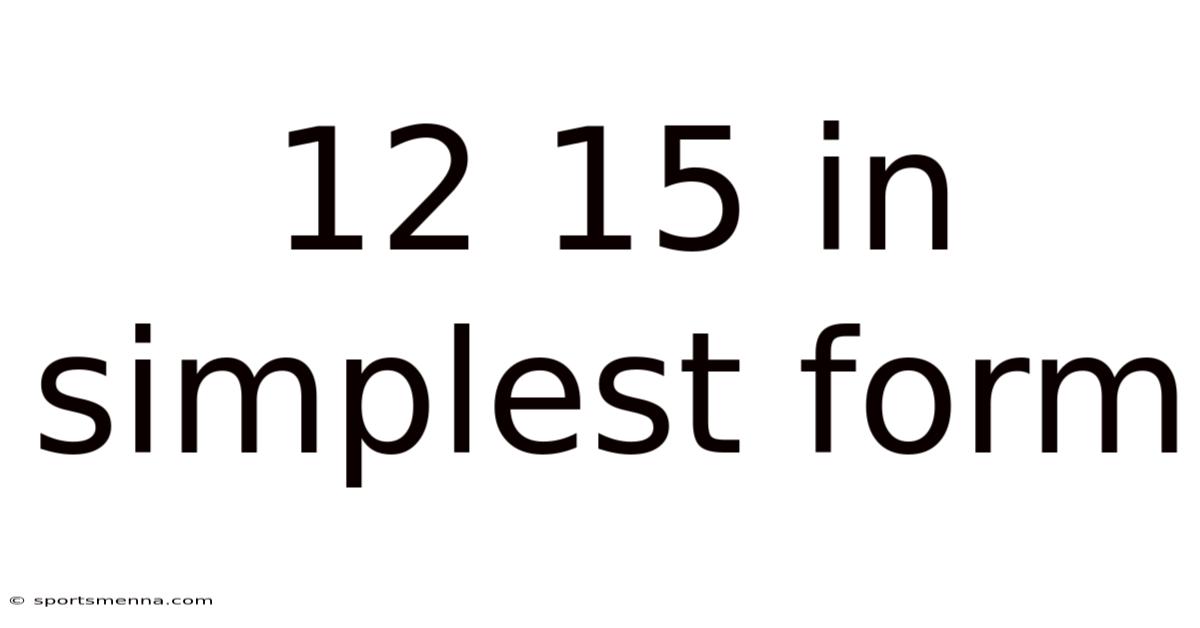
Table of Contents
Simplifying Fractions: A Deep Dive into 12/15
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will explore the simplification of the fraction 12/15, providing a comprehensive guide suitable for learners of all levels. We'll delve into the process, explain the underlying mathematical principles, and address common questions surrounding fraction simplification. By the end, you'll not only know the simplest form of 12/15 but also possess a robust understanding of how to simplify any fraction.
Introduction: What Does Simplifying a Fraction Mean?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. In essence, we're finding the smallest possible representation of the same fractional value. This makes the fraction easier to understand and work with in calculations. For instance, simplifying a fraction like 12/15 makes it easier to compare with other fractions or to perform operations like addition and subtraction.
Finding the Greatest Common Factor (GCF)
The key to simplifying a fraction lies in finding the greatest common factor (GCF) of the numerator and denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder. Let's find the GCF of 12 and 15.
Several methods exist for finding the GCF:
-
Listing Factors: List all the factors of 12 (1, 2, 3, 4, 6, 12) and all the factors of 15 (1, 3, 5, 15). The largest number appearing in both lists is the GCF. In this case, the GCF of 12 and 15 is 3.
-
Prime Factorization: Break down both numbers into their prime factors. The prime factors are the numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- 12 = 2 x 2 x 3 (2² x 3)
- 15 = 3 x 5
The common prime factor is 3. Therefore, the GCF is 3.
-
Euclidean Algorithm: This method is particularly useful for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCF.
- Divide 15 by 12: 15 ÷ 12 = 1 with a remainder of 3.
- Divide 12 by 3: 12 ÷ 3 = 4 with a remainder of 0.
The last non-zero remainder is 3, so the GCF is 3.
Simplifying 12/15
Now that we know the GCF of 12 and 15 is 3, we can simplify the fraction:
Divide both the numerator and the denominator by the GCF:
12 ÷ 3 = 4 15 ÷ 3 = 5
Therefore, the simplest form of 12/15 is 4/5.
Visual Representation
Imagine you have 12 slices of pizza out of a total of 15 slices. You can group these slices into sets of 3. You'll have 4 groups of 3 slices from the 12 slices and 5 groups of 3 slices from the 15 slices. Each group represents the same portion of the pizza, resulting in 4/5 of the pizza. This visual representation helps solidify the understanding of fraction simplification.
Explaining the Mathematical Principle
Simplifying a fraction is based on the fundamental principle of equivalent fractions. Multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction. We use this principle to find an equivalent fraction with the smallest possible whole numbers in the numerator and denominator. By dividing both 12 and 15 by their GCF (3), we are essentially dividing the fraction by 1 (3/3 = 1), which doesn't change its value.
Working with Larger Numbers
The same principles apply when simplifying fractions with larger numbers. For instance, let's consider simplifying 72/108:
-
Find the GCF of 72 and 108. Using prime factorization:
- 72 = 2³ x 3²
- 108 = 2² x 3³
The common prime factors are 2² and 3², so the GCF is 2² x 3² = 4 x 9 = 36.
-
Divide both the numerator and denominator by the GCF:
72 ÷ 36 = 2 108 ÷ 36 = 3
Therefore, 72/108 simplifies to 2/3.
Common Mistakes to Avoid
-
Dividing by the wrong number: Ensure you are dividing both the numerator and the denominator by their GCF, not just any common factor.
-
Not finding the GCF: Failing to identify the greatest common factor will result in an incomplete simplification. Always strive to find the largest common factor to obtain the simplest form.
-
Incorrect prime factorization: Errors in prime factorization will lead to an incorrect GCF and an incorrectly simplified fraction. Double-check your prime factorization to avoid these errors.
Frequently Asked Questions (FAQ)
Q: Is there more than one simplest form for a fraction?
A: No, a fraction has only one simplest form. If you obtain a different result, it indicates an error in the simplification process.
Q: What if the numerator and denominator have no common factors other than 1?
A: The fraction is already in its simplest form. For example, 7/11 is already simplified because 7 and 11 have no common factors other than 1.
Q: Can I simplify fractions with decimals?
A: It's best to convert decimals to fractions before simplifying. For example, if you have 0.75/1.5, convert them to 3/4 and 3/2 respectively, then simplify the resulting fraction 3/4 divided by 3/2 which would equal 1/2.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes calculations easier, improves understanding of the fractional value, and allows for easier comparison of fractions. It is a fundamental step in many mathematical operations and problem-solving scenarios.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a core mathematical skill that builds a solid foundation for more advanced concepts. By understanding the concept of the Greatest Common Factor and employing the methods outlined in this article, you can confidently simplify any fraction. Remember to always double-check your work and practice regularly to enhance your proficiency. The process of simplifying 12/15 to 4/5 serves as a practical example of this essential skill, highlighting the importance of finding the GCF and understanding equivalent fractions. This knowledge empowers you to tackle more complex problems with ease and accuracy. The ability to simplify fractions fluently will significantly improve your understanding and application of fractions in various mathematical contexts. Through practice and a solid understanding of the underlying principles, you can master this essential mathematical skill and confidently move on to more advanced topics.
Latest Posts
Latest Posts
-
A Vegetable Starting With A
Sep 21, 2025
-
170 Degrees C To Fahrenheit
Sep 21, 2025
-
Convert 10 Stone To Kilograms
Sep 21, 2025
-
Origin Of The Name Mann
Sep 21, 2025
-
Cities That Start With R
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 12 15 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.