1 1 X 1 2
sportsmenna
Sep 20, 2025 · 6 min read
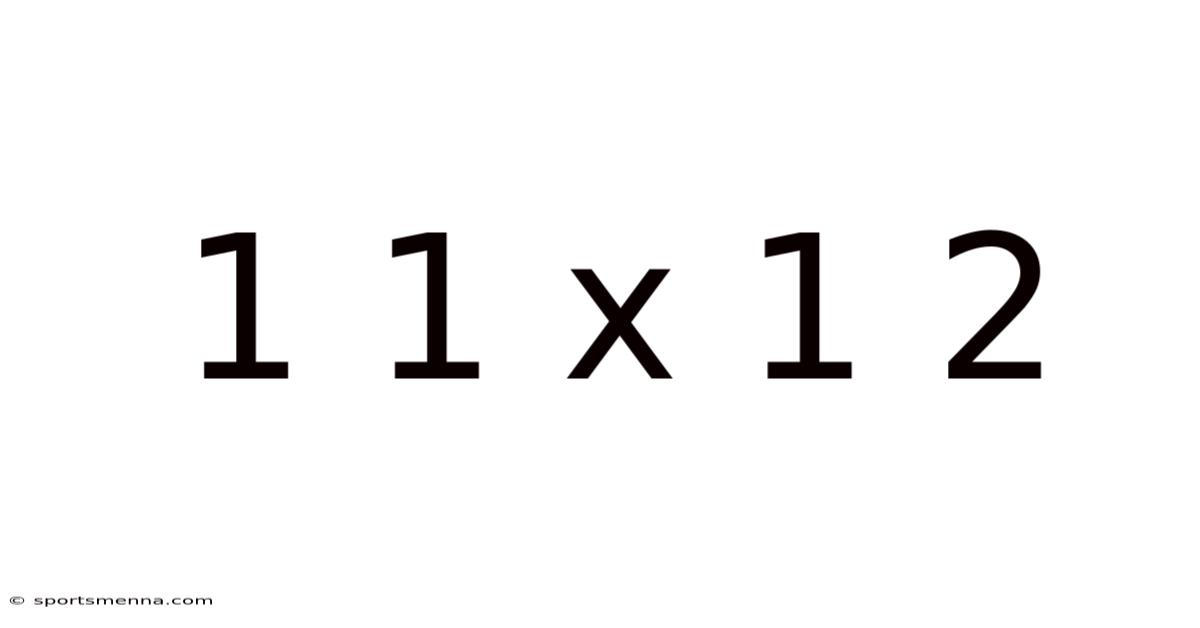
Table of Contents
Decoding 11 x 12: A Deep Dive into Multiplication and its Applications
Understanding multiplication is a cornerstone of mathematics, forming the basis for more complex calculations and problem-solving. This article delves into the seemingly simple calculation of 11 x 12, exploring the various methods for solving it, its underlying mathematical principles, and its practical applications in everyday life and various fields. We'll move beyond simply stating the answer (which is 132) and unravel the richness of this fundamental arithmetic operation.
Introduction: More Than Just a Number
At first glance, 11 x 12 might appear trivial. However, this seemingly simple multiplication problem offers a fertile ground for exploring different approaches to calculation, reinforcing fundamental mathematical concepts, and highlighting the interconnectedness of various mathematical areas. This exploration is vital for building a strong mathematical foundation, crucial for success in higher-level mathematics and numerous real-world applications. We will examine various methods to solve this problem, from traditional methods to more advanced techniques, ultimately revealing the deeper mathematical significance behind this simple equation.
Method 1: Standard Multiplication Algorithm
This is the most common method taught in schools. It involves multiplying each digit of the multiplicand (12) by each digit of the multiplier (11) and then adding the partial products.
- Step 1: Multiply 12 by the units digit of 11 (which is 1): 12 x 1 = 12. Write this down.
- Step 2: Multiply 12 by the tens digit of 11 (which is 1), placing the result one place value to the left: 12 x 10 = 120. Write this down below the first result, aligning the digits correctly.
- Step 3: Add the partial products: 12 + 120 = 132.
Therefore, 11 x 12 = 132. This method is straightforward and provides a solid foundation for understanding the distributive property of multiplication.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down the multiplication into smaller, easier-to-manage steps:
- Rewrite 11 as (10 + 1).
- Now, the equation becomes (10 + 1) x 12.
- Applying the distributive property: (10 x 12) + (1 x 12) = 120 + 12 = 132.
This method showcases an important mathematical concept and provides a more nuanced understanding of multiplication beyond rote memorization. It's particularly useful when dealing with larger numbers.
Method 3: Lattice Multiplication
Lattice multiplication is a visual method that can be helpful for understanding the underlying process of multiplication. It's particularly useful for multiplying larger numbers.
- Step 1: Draw a grid with two rows (for the two digits of 12) and two columns (for the two digits of 11).
- Step 2: Write the digits of 12 along the top and the digits of 11 along the right side.
- Step 3: Multiply each digit pair and write the result in the corresponding cell, separating tens and units digits diagonally.
- Step 4: Add the numbers along the diagonals, carrying over any tens to the next diagonal. This gives you the final answer.
This method, while seemingly more complex, offers a visual representation of the multiplication process and can be beneficial for students who struggle with the standard algorithm.
Method 4: Mental Math Techniques
For those aiming to improve their mental calculation skills, there are several techniques to solve 11 x 12 mentally:
- Breaking it down: Think of 11 as 10 + 1. Then, 10 x 12 = 120, and 1 x 12 = 12. Add those together: 120 + 12 = 132.
- Using doubling and halving: Double 11 to get 22, and halve 12 to get 6. Then, multiply 22 x 6, which might be easier to calculate mentally: 22 x 6 = 132. This method relies on the commutative property of multiplication (a x b = b x a).
- Remembering multiplication facts: If you know your multiplication tables well, you might instantly recall that 11 x 12 = 132. Regular practice and memorization are key to achieving this.
These mental math techniques are valuable for enhancing mathematical fluency and problem-solving agility.
The Mathematical Principles at Play
The simple calculation of 11 x 12 illustrates several fundamental mathematical principles:
- Commutative Property: The order of the numbers doesn't matter: 11 x 12 = 12 x 11.
- Associative Property: When multiplying more than two numbers, the grouping doesn't affect the product. (This isn't directly applicable to just 11 x 12, but it's crucial for understanding multiplication in more complex scenarios).
- Distributive Property: This property, as explained earlier, allows us to break down the multiplication into smaller, manageable parts.
- Place Value: Understanding place value is essential in the standard multiplication algorithm, ensuring the correct alignment of digits during the addition of partial products.
Mastering these properties is key to developing a solid understanding of arithmetic and algebra.
Real-World Applications
While seemingly simple, multiplication finds its way into numerous real-world situations:
- Shopping: Calculating the total cost of multiple items. If you buy 11 items at $12 each, you'll spend $132.
- Construction: Calculating the area of a room (length x width).
- Cooking: Scaling recipes. If a recipe calls for 12 ounces of an ingredient and you want to make 11 servings, you'll need 132 ounces.
- Finance: Calculating interest, taxes, or discounts.
- Engineering: Numerous engineering calculations rely heavily on multiplication.
- Data Analysis: Multiplication is vital in many statistical and data analysis processes.
These examples highlight the ubiquity of multiplication in our daily lives and various professions.
Expanding the Concept: Beyond 11 x 12
Understanding 11 x 12 allows us to extend this knowledge to more complex problems. For example, we can use this knowledge to solve problems involving larger numbers or more complex operations:
- Multiplying larger numbers: Understanding the fundamental principles of multiplication, as demonstrated with 11 x 12, allows us to tackle larger multiplication problems efficiently and accurately.
- Solving algebraic equations: The principles of multiplication are integral to solving algebraic equations and inequalities.
- Working with fractions and decimals: The same principles apply when dealing with fractions and decimals.
The seemingly simple 11 x 12 serves as a building block for more sophisticated mathematical concepts and real-world applications.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate 11 x 12?
A: The easiest way depends on your preference and skill level. The standard algorithm is reliable, while the distributive property or mental math techniques might be quicker for those comfortable with them.
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental mathematical operation crucial for various calculations and problem-solving across many disciplines and everyday situations.
Q: Are there any tricks to memorize multiplication facts quickly?
A: Yes, various memory techniques and regular practice can help memorize multiplication facts effectively. Flashcards, online games, and repeated drills can be beneficial.
Q: How can I improve my mental math skills?
A: Consistent practice with mental math exercises, focusing on different techniques and strategies, significantly improves your mental calculation abilities.
Q: How does multiplication relate to other mathematical concepts?
A: Multiplication is closely linked to addition, division, algebra, geometry, calculus, and numerous other mathematical areas.
Conclusion: The Significance of a Simple Equation
The seemingly simple multiplication problem, 11 x 12, serves as a gateway to a deeper understanding of mathematical principles and their real-world applications. By exploring various methods of solving this problem and understanding the underlying mathematical concepts, we have unveiled the richness and significance of a fundamental arithmetic operation. Mastering this simple calculation forms a strong foundation for more advanced mathematical concepts and problem-solving, empowering individuals to tackle complex challenges in various fields and everyday life. The journey from 11 x 12 to a comprehensive grasp of mathematical principles is a testament to the power of foundational knowledge and its far-reaching implications.
Latest Posts
Latest Posts
-
Natwest Pigs Full Set Value
Sep 21, 2025
-
How Many Inches Is 137cm
Sep 21, 2025
-
Ml In Half A Pint
Sep 21, 2025
-
1 Fluid Ounce To Liters
Sep 21, 2025
-
Highest Two Digit Prime Number
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1 1 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.